Na primeira parte deste artigo analisamos diversos aspectos que envolvem o funcionamento de um analisador de espectro FFT, para que os leitores que precisam entender os recursos desse tipo de equipamento saibam quais são suas limitações e possibilidades. Vimos na ocasião que um dos fenômenos ue afetava a precisão das medidas era o “alias”. Nesta segunda parte de nosso artigo veremos o porque usar um filtro e também como empregar alguns recursos de “janelas” com esse instrumento. Lembramos que o artigo é baseado em documentação da Agilent Technologies.
Por que usar um Filtro Anti-Alias?
No mundo real os sinais não estão restritos a uma faixa de freqüências pequena.
Os sinais da rede de energia, por exemplo, podem conter harmônicas que se estendem para muito além do que pode alcançar a capacidade de manuseio de um circuito de amostragem.
Para evitar que freqüências que estejam acima da capacidade de manuseio dos circuitos, e que poderiam falsear os resultados, é preciso usar um filtro anti-alias, conforme mostra a figura 1.
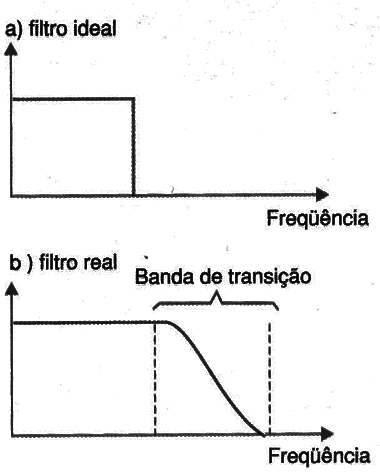
Esse filtro, conforme sugere a figura 2, deixa passar sem atenuação os sinais das freqüências que devem ser analisadas, impedindo a passagem dos sinais que poderiam falsear os resultados.
Conforme podemos ver, como não é possível construir um filtro ideal, o que temos é uma atenuação a partir de uma certa freqüência, obtendo-se assim uma banda de transição.
Um sinal muito forte que não sejam devidamente atenuados, podem ainda ter componentes fortes na banda de transição, as quais não são totalmente atenuadas, causando assim erros.
Mais de um Filtro
Conforme vimos, a taxa de amostragem depende da freqüência do sinal de amostrado de modo a se evitar o espalhamento de freqüências de um analisador.
Para reduzir o espalhamento de freqüência, deve-se reduzir a taxa de amostragem, o que significa que também é preciso reduzir a freqüência do filtro anti-alias na mesma proporção.
Como os analisadores de espectro são construídos para operar numa faixa muito ampla de freqüências, é necessário que eles possuam recursos para também poderem reduzir o espalhamento de freqüência.
Os analisadores típicos possuem espalhamentos de 1 Hz até um máximo de dezenas ou centenas de quilohertz.
Uma faixa de quatro décadas deve ser coberta com pelo menos três espalhamentos por década. Isso significa a existência de pelo menos 12 filtros anti-alias para cada canal.
Esses filtros devem ter excelente performance.
Suas bandas de transição devem ser as mais estreitas possíveis, de tal forma que produtos anti-alias sejam reduzidos ao máximo.
Filtragem Digital
Uma alternativa que é mais simples e barata para a filtragem, e que pode ser usada com um único filtro anti-alias, pode resultar em bom desempenho para os analisadores. Essa alternativa faz uso de “filtros digitais”.
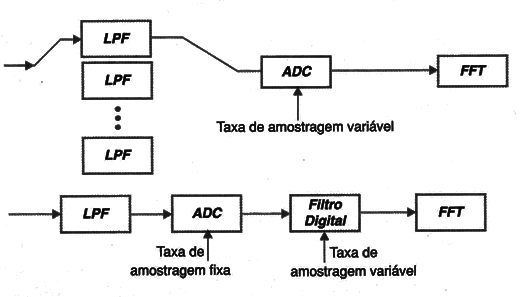
Esses filtros trabalham com os sinais depois que eles são digitalizados, conforme mostra a figura 3.
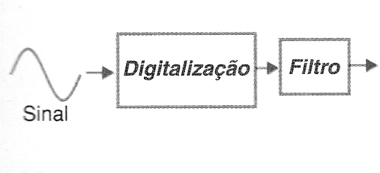
Quando o circuito de filtragem usado é analógico, deve ser usado um novo filtro cada vez que a taxa de amostragem do ADC muda.
Para a filtragem digital, a taxa de amostragem do ADC é mantida constante na velocidade exigida pelo espalhamento da componente de maior freqüência do sinal.
Esse tipo de filtro é conhecido como “filtro de decimação”, porque ele não apenas filtra a representação digital do sinal para o espalhamento desejado de freqüências, como também reduz a taxa de amostragem em sua saída para o valor para o espalhamento de freqüência necessário.
Assim, num analisador de dois canais, os filtros dos dois canais são iguais, tornando mais fácil o projeto para operação em muitas freqüências.
Levando em conta tudo isso, o uso do filtro digital significa economia, quando comparado com a solução analógica.
Análise de Banda Selecionável
Imagine que você precisa analisar um sinal que tenha uma freqüência muito próxima de um outro que é muito mais forte.
Por exemplo, desejamos medir a componente de 60 Hz da rede de energia presente num sinal de 20 kHz.
Levando em conta o que vimos da FFT, que nos mostra que ela se comporta como um conjunto de filtros, partindo de zero hertz e com freqüências igualmente espaçadas podemos entender melhor como fazer isso.
Vemos que em função disso, a resolução de freqüência que obtemos é limitada à freqüência máxima dividida pelo número de filtros.
Assim, para resolver as bandas laterais de 60 Hz num sinal de 20 kHz, precisaremos de 333 linhas (ou filtros) do FFT.
Duas ou mais linhas serão necessários para medir com precisão as linhas laterais.
Os analisadores dinâmicos típicos possuem entre 200 e 400 linhas de resolução, o que não é suficiente para medidas precisas.
Para aumentar o número de linhas, o custo do instrumento aumentaria de modo significativo.
Mesmo se estivéssemos dispostos a pagar a diferença, haveria ainda um problema a considerar: com um display de 10 cm as bandas laterais estariam 0,25 mm apenas separadas da portadora.
Uma maneira melhor de resolver o problema é concentrar os filtros numa faixa de freqüências mais estreita que seja do nosso interesse, conforme mostra a figura 4.
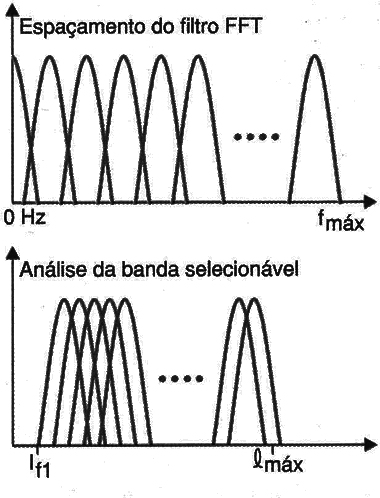
Se escolhermos de modo apropriado a freqüência mínima e a freqüência máxima, podemos ter um efeito de “zoom” na parte do sinal que nos interessa.
Essa capacidade é denominada “band selectable analysis” ou PSA, que em português poderia ser traduzido como analise de banda selecionável.
Esse recurso é implementado mixando ou heterodinando o sinal de entrada, de modo a baixar sua freqüência para o espalhamento FFT selecionado.
Esse processo é semelhante ao que se faz com sinais de rádio em receptores super-heteródinos.
No FFT, entretanto, existem algumas diferenças, conforme mostra a figura 5.
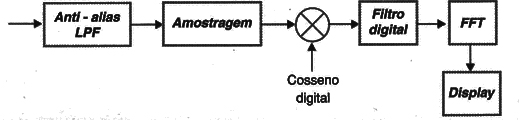
Num receptor de rádio, o mesmo sinal é usado para mixar uma tensão analógica.
Num analisador dinâmico, a mixagem é feita depois que a entrada foi digitalizada.
Dessa forma, o sinal senoidal adicionado é uma série de número digitais aplicados a um circuito multiplicador.
Isso significa que o resultado da mixagem é um sinal digital muito preciso e estável.
Windowing
“Windowing” ou “janelar” e ó termo usado para indicar a abertura de uma janela na tela do instrumento para se observar em detalhes uma parte do sinal que está sendo analisado.
Esse recurso é importante, pois existe uma propriedade da Fast Fourier Transform ou Transformada Rápida de Fourier que afeta o seu uso na análise do domínio de freqüências.
Lembramos que na FFT computa-se o espectro de freqüências de um bloco de amostras de entrada obtida em um certo intervalo de tempo.
Além disso, o algoritmo da FFT é baseado no fato de se assumir que o tempo registrado se repete ao longo do tempo, conforme mostra a figura 6.
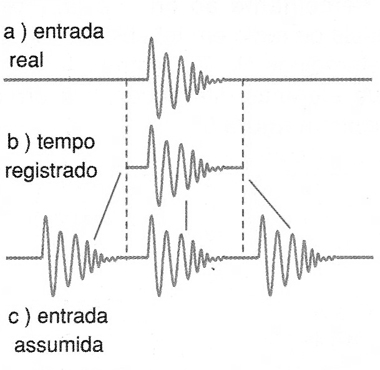
Isso não é problema para o caso de um transiente como o mostrado na figura 1. Mas, o que ocorre se o sinal medido for uma onda contínua, um sinal senoidal, por exemplo?
Se o tempo de amostragem contiver um número inteiro de ciclos do sinal de entrada, então assume-se que a imagem apresentada corresponde exatamente ao sinal amostrado, conforme mostra a figura 7.
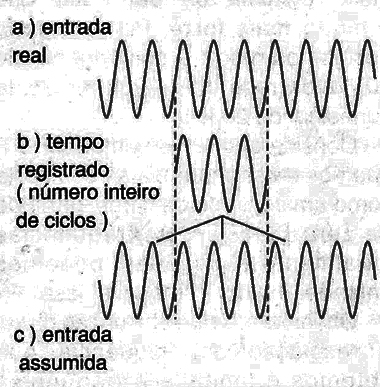
Quando isso ocorre diz-se que a forma de onda de entrada é “periódica” no intervalo registrado.
No entanto, isso não ocorre sempre, já que existe a dificuldade de se ter a amostragem exatamente começando no início de um ciclo, conforme mostra a figura 8 e com isso, um número inteiro de ciclos do sinal de entrada.
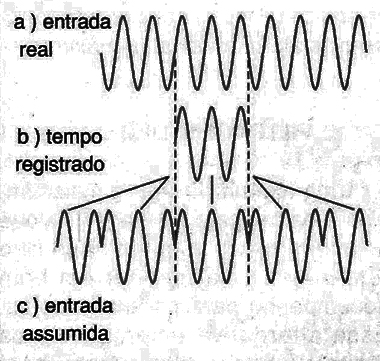
Nesse caso não temos uma forma de onda periódica, aparecendo na tela do instrumento um sinal distorcido.
Evidentemente, o espectro desse sinal amostrado não corresponde ao sinal anterior, apesar de serem os mesmos!
Está claro que correto é que o sinal seja periódico ao ser amostrado de modo que o espectro obtido corresponde ao real.
O que é “windowing”?
Na figura 9 temos novamente uma amostragem do que ocorre quando uma forma de onda senoidal não é Periódica em relação ao tempo de registro.
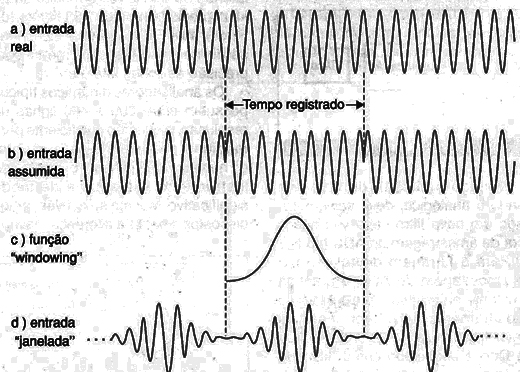
Observe que a maior parte do problema parece residir nos instantes em que o registro é feito. Se a FFT puder ser elaborada de modo a ignorar os extremos e se concentrar apenas no meio do intervalo do sinal registrado, podemos ter uma aproximação muito melhor do espectro real do sinal no domínio de freqüências.
Assim, o que se faz é multiplicar o tempo registrado por uma função que seja zero nas extremidades do domínio de tempo registrado e tenha um valor maior no centro.
Com isso, conforme mostra a figura 4(c) teremos uma concentração da FFT no centro do intervalo de tempo registrado.
Essas funções são denominadas “funções janela” ou “window function” porque elas forçam a análise ou observação do sinal numa “janela” mais estreita.
Qualquer número de funções pode ser usado para “janelar” dados, mas a mais comum é a denominada “Hanning”. Essa função, pelas suas características é mais usada para se observar ruídos.
No caso do sinal senoidal tomado como exemplo nesse artigo, também foi usada essa função.
Na continuação
As “funções janela” são muito importantes quando se analisam sinais complexos.
Na última parte deste artigo, INS243, veremos quais são os tipos de funções janela e quando utilizá-las.