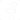Os filtros encontram uma grande gama de aplicações práticas na eletrônica. Separando sinais de frequências indesejáveis das desejáveis, estes circuitos podem ser usados de inúmeras formas implementando aparelhos diversos como acionadores seletivos, eliminadores de interferências, separadores de sons etc. Neste artigo falamos especificamente dos filtros com amplificadores operacionais em função das características adicionais que o AO como elemento ativo pode proporcionar.
Dizemos que um filtro é passivo quando ele é composto apenas de componentes passivos como resistores, capacitores, indutores etc.
Num filtro passivo, dada a não existência de dispositivos amplificadores, a energia do sinal obtido na saída é sempre menor do que a aplicada na entrada.
A diferença entre as duas energias determina a perda que ocorre no filtro e em alguns casos ela é tão grande que impede até a utilização prática do dispositivo ou pelo menos a limita.
No entanto, resistores, capacitores e indutores mais um elemento ativo como um amplificador operacional podem mudar de figura o comportamento do filtro.
Além da atuação sobre determinadas frequências podemos ainda ter um ganho de intensidade para o sinal, o que nos leva aos chamados filtros ativos.
Temos então os seguintes tipos de filtros que podem ser elaborados com a ajuda de amplificadores operacionais:
- Filtros passa-baixas que deixam passar os sinais de baixas frequências até um valor limite determinado por suas características.
- Filtros passa-altas que deixam passar os sinais de altas frequências até um valor limite determinado por suas características.
- Filtros passa-banda ou passa-faixa que deixam passar apenas os sinais de uma faixa determinada de frequências.
- Filtros rejeitores de faixa ou de banda que deixam passar sinais de todas as frequências menos os compreendidos entre dois limites bem estabelecidos.
Na figura 1 temos a representação destes filtros.
FILTROS DE GANHO UNITÁRIO
Estes são os mais simples de serem projetados, combinando um amplificador operacional como seguidor de tensão com uma rede RC que proporciona as características de resposta relativa à frequência do sistema.
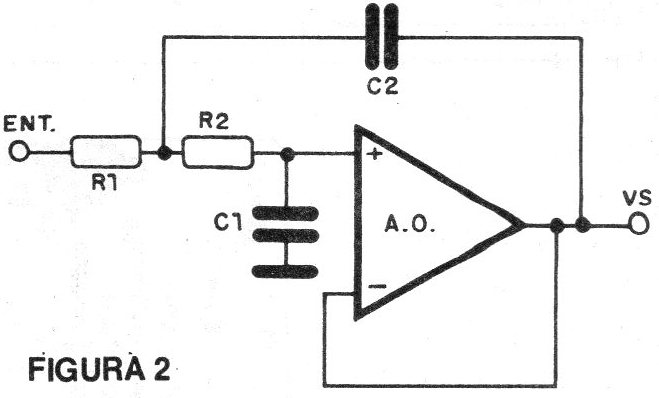
Na figura 2 temos um filtro passa-baixas em que apenas 2 resistores e dois capacitores são utilizados.
A fonte de alimentação deve ser simétrica e as equações que proporcionam a frequência a partir dos valores dos componentes para uma atenuação de -3dB são:
a) Frequência inferior de corte:
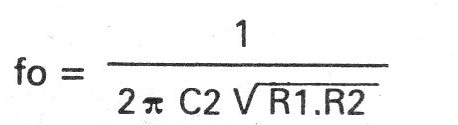
b) Frequência superior de corte:
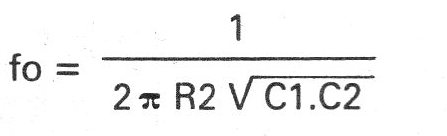
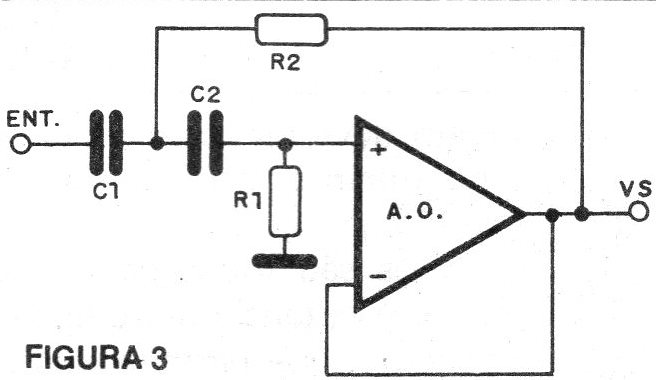
Na figura 3 temos a configuração para um filtro passa-altas onde que se aplica as mesmas fórmulas.
O fator de seletividade (fator Q), entretanto, é calculado para os dois circuitos de formas diferentes:
Para o filtro passa baixas temos:
Q =1/2 V C1/C2
Para o filtro passa-altas temos:
Q =1l2 V R1/R2
(As fórmulas são válidas para fatores Q maiores que 10)
FILTROS ATIVOS PASSA-BAIXAS
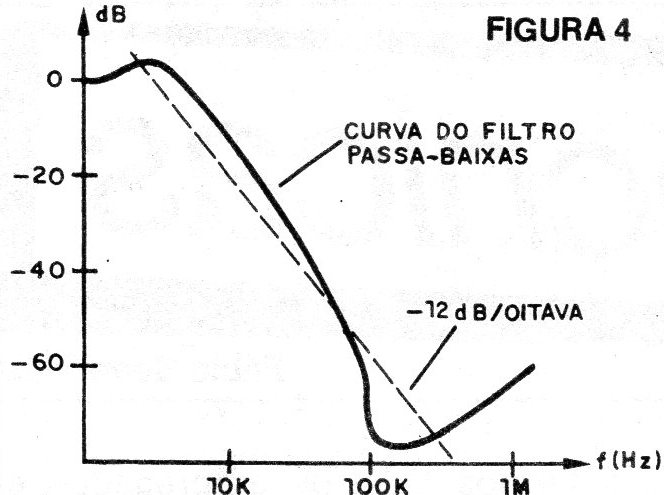
Na figura 4 temos a curva de um amplificador operacional típico usado como filtro passa-baixas.
Na prática a atenuação de 12 dB por oitava obtida pode ter valores menores com frequências mais altas.
Um amplificador operacional ideal tem impedância de entrada infinita, impedância de saída nula e ganho infinito para sinais de quaisquer frequências.
Na prática, estas características estão longe do ideal o que os torna próximos de um comportamento bom até frequências em torno de 100 kHz.
Acima desta frequência as características de impedâncias de entrada e saída começam a ter valores que não devem ser desprezados nos cálculos.
Amplificadores operacionais de banda larga da Texas como o LM318 ou TL291, podem ser usados em frequências mais altas com eficiência.
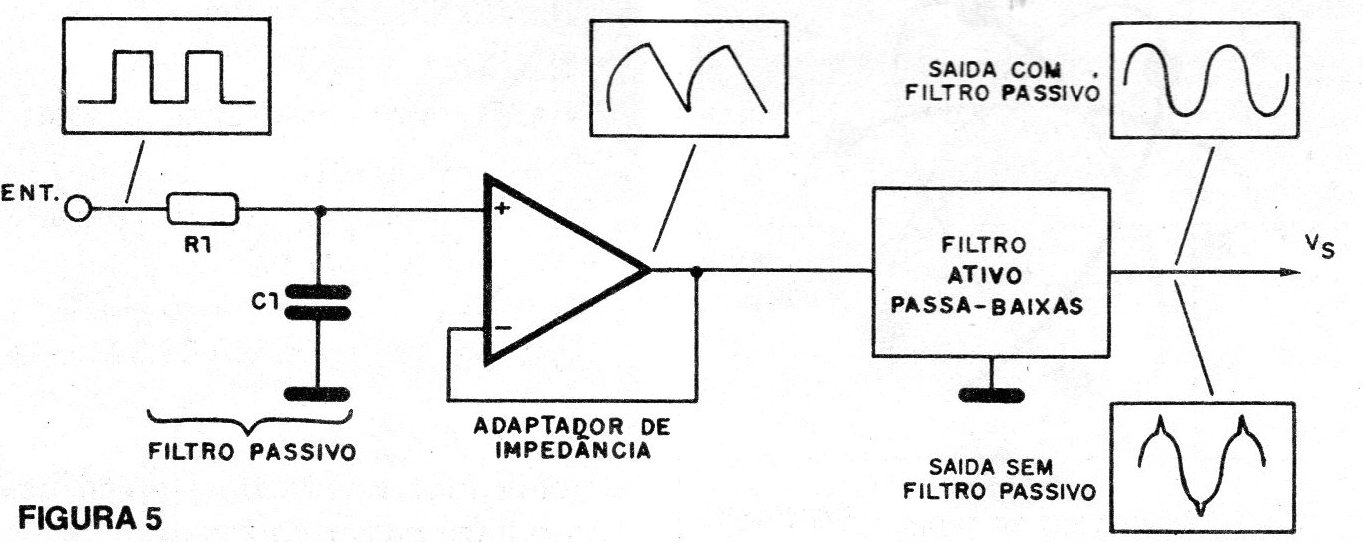
Uma maneira de se obter melhor comportamento nas altas frequências consiste na utilização de um filtro passivo RC antes do filtro ativo, conforme mostra a figura 5.
Neste caso, entretanto, um casador de impedância deve ser intercalado para que sejam evitadas perdas perigosas ao desempenho do sistema.
FILTROS REJEITORES DE BANDA
Estes são filtros ativos, com configuração típica mostrada na figura 6 em que empregamos um amplificador operacional 741.
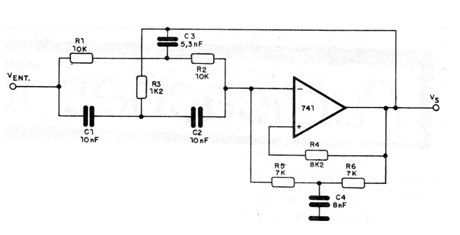
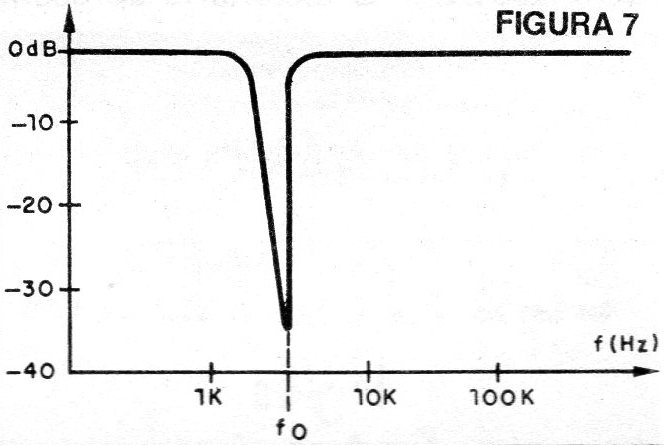
A curva de resposta deste filtro é mostrada na figura 7.
Trata-se de um filtro rejeitor de banda de segunda ordem com frequência centralizada em 3 kHz.
O fator Q deste circuito e 23, com uma atenuação no ponto de máximo de -31 dB.
Pode-se obter uma resposta muito mais aguda para este filtro com a utilização de circuitos LC em lugar do duplo T com resistores e capacitores. Igualmente, aumenta-se a atenuação no ponto de ressonância com a utilização de capacitores de altos valores.
FILTROS ATIVOS PASSA-BANDA
Num filtro deste tipo, temos a passagem de uma faixa de frequências situada entre dois limites muito bem estabelecidos.
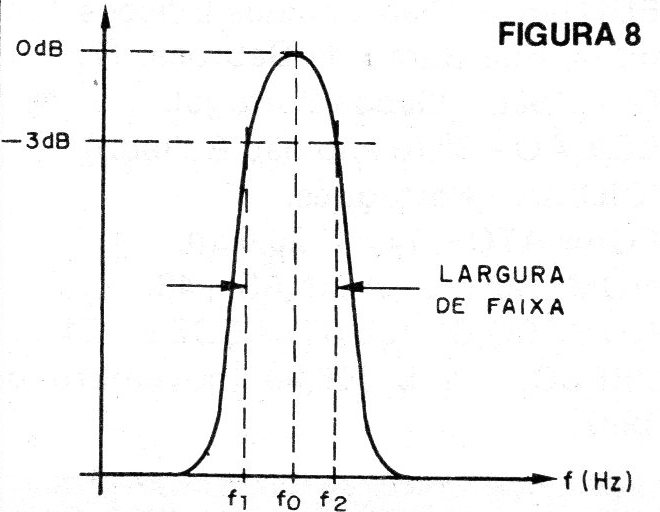
Chamamos de fo a frequência central, ou seja, a frequência em torno da qual é limitada a faixa de sinais que passa e a frequência para a qual o ganho de tensão é máximo. (figura 8)
A largura de faixa para este tipo de filtro é definida para os pontos antes e depois da frequência central na qual o ganho cai a 0,707 do máximo, ou seja, em que se tem uma atenuação de 3dB em relação ao valor da tensão em fo.
Os valores fL e fH correspondem aos limites inferiores e superiores respectivamente da faixa passante.
Assim, a faixa é dada por:
BW = fH – fL
A partir destas frequências definimos o fator Q como:
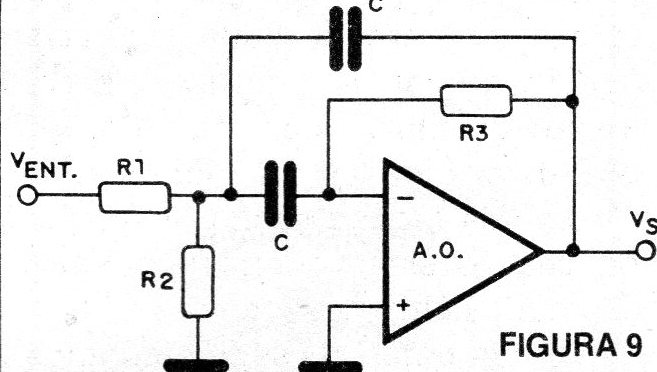
Na figura 9 temos a configuração de um filtro deste tipo com amplificador operacional.
Este filtro tem características que permitem sua utilização com fatores Q até 10.
Os valores de C típicos para aplicações em áudio devem ficar entre 10 nF e 100nF. A partir destes valores e da frequência central podemos calcular os demais componentes pelas fórmulas:
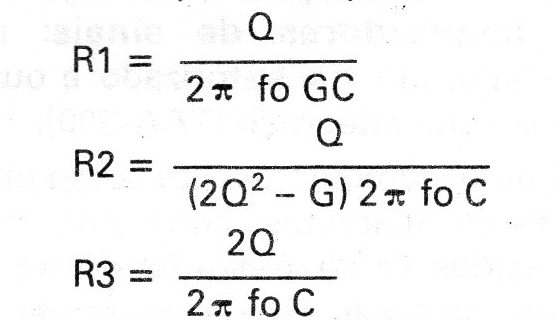
A melhor performance do circuito é obtida quando se faz o ganho maior que a raiz quadrada de Q.
Por exemplo, se o filtro for projetado para um fator Q de 16, então o ganho deve ser maior que 10.
Ref.: Linear and Interface Circuits Applications - Texas lnstruments - 1985.