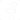Nas lições anteriores aprendemos como funcionam os computadores analógicos e especificamente como potenciômetros podem ser usados para construir um computador simples capazes de executar operações básicas usadas em matemática.
Logo em seguida, aprendemos como montar um circuito prático de um pequeno computador experimental capaz de fazer diversas operações. Na análise básica de seu funcionamento ficou claro como podemos fazer multiplicações. Nesta lição mostraremos como fazer outras operações.
Revisaremos, entretanto a operação da multiplicação mostrando como ela pode ser feita.
a) Multiplicação
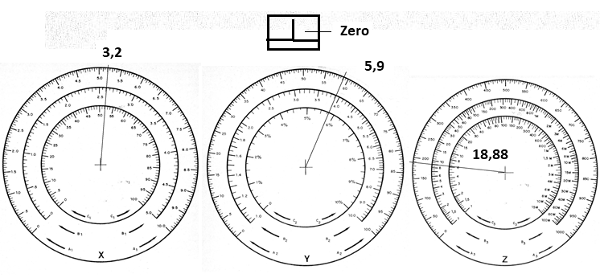
Vamos supor que desejamos fazer uma multiplicação simples como 3,2 x 5,9;
Neste caso temos:
X = 3,2
Y = 5,9
Z = resultado da operação
O primeiro procedimento é colocar na escala o valor da forma que seja mais próxima que a escala usada suporte. Observe que a escala linear vai até 10. Assim, temos na figura o ajuste de X para este valor.
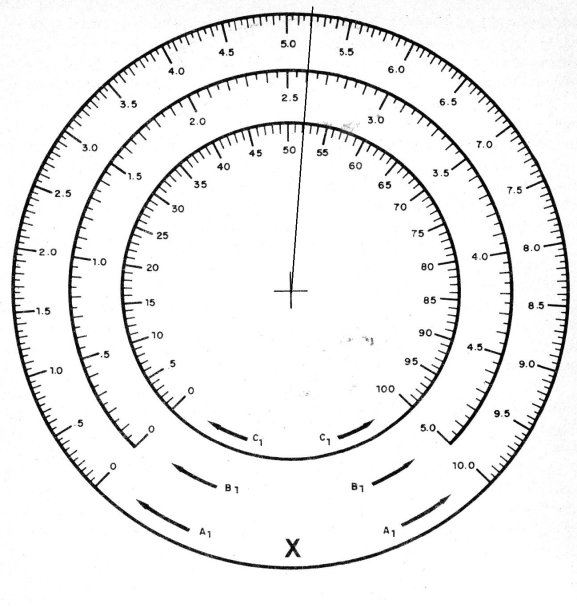
O segundo passo é ajustar o valor 5,9 na escala Y. Procedemos da mesma forma como na escala X, conforme mostra a figura 2.
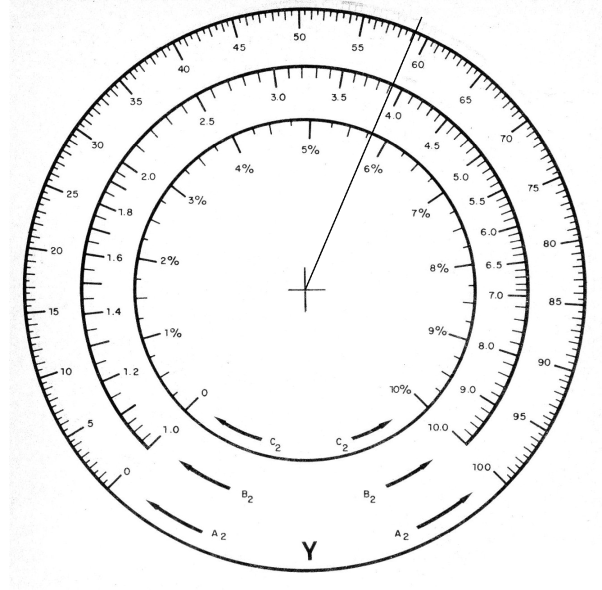
Veja que ajustaríamos esse mesmo ponto se tivéssemos que trabalhar com números maiores, compensando os zeros. Por exemplo, isso seria valido para a multiplicação: 32 x 59 = Y
Agora, na etapa final, vamos acionar o circuito e girar Z até que o instrumento seja zerado. Isso ocorrerá justamente no ponto 18,88, conforme mostra a figura 3.
Veja que neste caso temos de fazer uma compensação das escalas, deduzindo de cabeça que o valor encontrado esta aproximadamente neste ponto e que devemos desconsiderar um zero no resultado da operação.
Como nas réguas de cálculo, a ordem de grandeza tanto dos operandos como dos valores encontrados depende muito mais do operador do que do próprio dispositivo usado no cálculo.
Outro ponto importante a ser considerado é a precisão dos resultados. O valor 18,88 não poderá ser lido com precisão na escala externa usada da mesma forma que os valores dos operandos.
Assim, este tipo de calculadora não é para valores que exijam precisão, funcionando mais com pequenos valores inteiros. Leve-se em consideração a tolerância dos potenciômetros.
O resultado final é então mostrado na disposição final dos potenciômetros conforme detalha a figura 4.
Para as outras operações o procedimento é basicamente o mesmo, de modo que não precisaremos ilustrar com figuras. Apenas diremos quais as escalas usadas.
b) Divisão
Considerando que a divisão é um procedimento inverso ao da multiplicação o leitor pode facilmente deduzir como realizá-la em seu computador analógico.
Supondo que vamos dividir 9 por 2.
Neste caso, invertemos o procedimento, colocando o 90 na escala Z e o 20 na escala Y.
Z = 90
Y = 20
X = ?
O resultado será obtido na escala X quando girarmos o potenciômetro e conseguirmos o zeramento do instrumento.
Veja que também neste caso devemos considerar os pontos em que os valores serão ajustados.
Para 90 usamos 9, para 20 usamos 2 e o resultado não será obtido em 45 mas sim e 4,5.
c) Potencias
Elevar um número ao quadrado, consiste em multiplica-lo por ele mesmo. Por exemplo:
32 = 3 x 3 = 9
Assim, para elevar ao quadrado, basta ajustar o mesmo número na escala x e na escala Y encontrando a resposta na escala Z.
Elevar 4 ao quadrado, por exemplo:
X = 4
Y = 4
Encontraremos Z = 16 quando o instrumento for zerado.
Para outros expoentes já temos um procedimento que exige um pouco mais de habilidade. Por exemplo, vamos elevar 43.
Neste caso, temos:
4 x 4 x 4
Fazemos então a primeira multiplicação usando os potenciômetros x e y. Obtemos o valor 16 em Z. Ajustamos novamente Y para o valor encontrado em Z e novamente ajustamos Z para um novo zeramento.
O valor encontrado será 4 x 4 x 4 = 64 ou 43.
Para expoentes maiores também podemos usar as escalas intermediárias B trabalhando como se fossem multiplicações. Veja mais adiante porque isso é possível.
d) Raiz quadrada
A raiz quadrada de um número a é o número b que multiplicado por ele mesmo resulta em a.
Por exemplo, a raiz quadrada de 9 é 3 porque 3 x 3 = 9. A raiz quadrada de 16 é 4 porque 4 x 4 = 16.
Para calcular a raiz de um número no nosso comutador analógico usaremos as escalas da faixa intermediária B. Assim, se queremos calcular a raiz de 9, ajustamos 9 na escala B de X. Depois ajustamos novamente 9 na escala B de Y e encontramos o resultado aproximado na escala B de Z.
Porque o resultado das raízes são obtidos nessas escalas?
Para que o leitor entenda deve conhecer um pouco sobre logaritmos.
Se tivermos os números a, b e c e realizarmos a operação tal que ax = b, podemos dizer que x é o logaritmo de b na base a ou:
X = loga b
Uma escala logarítmicas em que as divisões são separadas de forma exponencial, tem propriedades interessantes quando usadas num computador como o nosso.
Por exemplo, vemos que a a soma dos logaritmos de dois números é igual ao logaritmo de seu produto. Em outras palavras, podemos multiplicar usando a soma.
Da mesma forma, para obter uma potência, basta multiplicar o logaritimo da base pelo logaritmo do expoente. Em outras palavras, podemos calcular expoentes usando a multiplicação.
Como a raiz quadrada é o inverso da potenciação, usando um escalas logarítmicas podemos fazer seu calculo usando a divisão.
Assim, a raiz quadrada de um número pode ser encontrada dividindo o logaritmo desse número pelo logaritmo de 2. As escalas B do nosso computador servem justamente para fazer esses cálculos usando logaritmos.
Mas, o interessante é que, como trabalhar com grandezas analógicas podemos ir muito além do que seria possível com uma calculadora digital.
Podemos elevar um número a um expoente não inteiro como 30,4 ou ainda a raiz “1,3” de 2.
Cálculos Complexos
É claro que, á medida que o leitor for adquirindo experiência com seu computador analógico pode ir entendendo como realizar mais cálculos. Por exemplo, pode criar novas escalas, colocando por exemplo funções trigonométricas e trabalhando com elas.
Basta lembrar que o circuito multiplica e que portanto podemos realizar esta operação com os valores das escalas. Se essas escalas forem elaboradas com base em outras funções as suas características é acrescentada ao circuito.
Por exemplo, se tivermos uma escala que siga a função “seno de um ângulo” em X e “cosseno” em Y poderemos multiplicar senos por cossenos, bastando elaborar uma escala apropriada em Z.
Outra possibilidade consiste em se modificar o modo como os potenciômetros são ligados. Na figura 5, por exemplo, temos uma variação que nos leva a fórmula de atuação do circuito como:
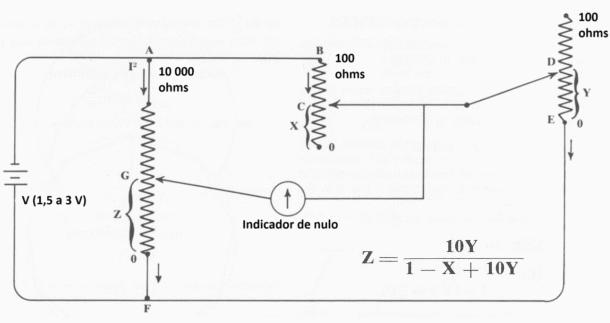
Um sistema de comutação interno pode levar ás diversas configurações do circuito.
Outra possibilidade interessante é mostrada na figura 6, sempre levando em conta que a relação de valores entre os potenciômetros de alta e de baixa resistência deve ser mantida a mais alta possível para se obter mais precisão.
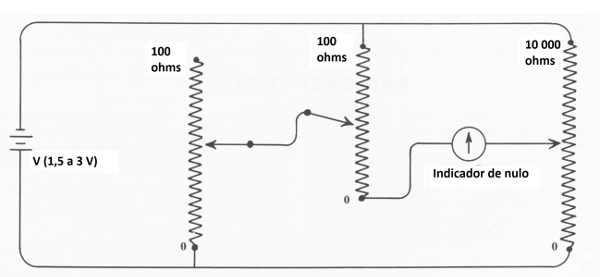
Analisando este circuito o leitor pode chegar a equação que descreve sua operação. Assim, da mesma forma que num computador analógico com amplificadores operacionais, disposições diferentes de potenciômetros podem ser criadas para realizar os cálculos específicos que desejamos.
Temos ainda a possibilidade de aumentar o número de potenciômetros, conforme mostra a figura 7.
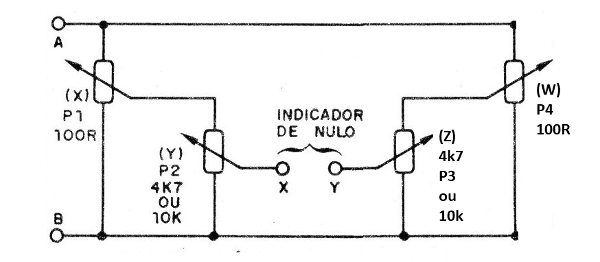
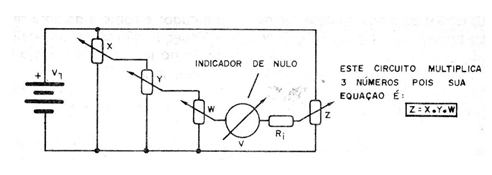
Veja que neste circuito temos a possibilidade de resolver equações do tipo:
X x Y = W x Z
Para operações simples, como as normais, basta colocar W no ponto de máxima resistência (Cursor em +B) da alimentação e circuito passa a ter a condição de Z = 1 levando a:
X x Y = Z x 1
Ou
X x Y = Z
Que é a versão original.
No entanto, a vantagem deste circuito é que podemos resolver proporções com ele, calculando por exemplo a quarta proporcional na fórmula:
X/Y = W/Z
Essa possibilidade de incrementar o projeto, certamente pode ser atraente para os leitores que desejarem saber mais sobre computadores analógicos.
Podemos até trabalhar com seis potenciômetros sendo 3 em cada ramo obtendo assim a equação de funcionamento:
X x Y x Z = X1 x Y1 x Z1
O terceiro potenciômetro de 100k ou 1 M seria ligado no cursor de Y.
Na figura 8 temos um circuito para X x Y x W = Z
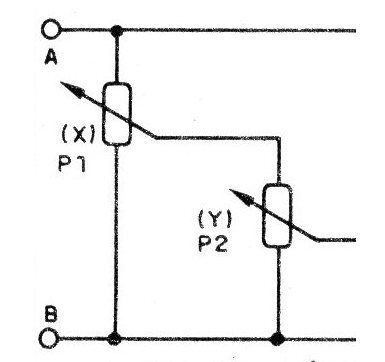
Devemos sempre lembrar que na escolha dos valores dos componentes o potenciômetro de carga (que carrega o divisor principal) deve ser o maior possível pelos motivos que já analisamos nas lições anteriores de nosso curso.
No circuito da figura 9 P2 deve ser o maior possível em relação a P1 para não “carregá-lo” formando um divisor de tensão que afeta os resultados do circuito.
Índice
Introdução à Computação Analógica (CUR6000)
Computação Analógica – Lição 1 – Os Computadores Analógicos (CUR6001)
Computação Analógica – Lição 2 – Os Componentes do Computador Analógico (CUR6002)
Computação Analógica – Lição 3 – Monte um Computador Analógico (CUR6003)