O que são capacitores
Os capacitores (que também são chamados erroneamente de condensadores pelos profissionais antigos) são componentes eletrônicos formados por conjuntos de placas de metal entre as quais existe um material isolante que define o seu tipo.
Assim, se o material isolante for a mica teremos um capacitor de mica, se for uma espécie de plástico chamado poliéster, teremos um capacitor de poliéster. Se for a cerâmica, teremos um capacitor cerâmico e assim por diante. Existem muitos materiais que podem ser usados para fabricar capacitores.
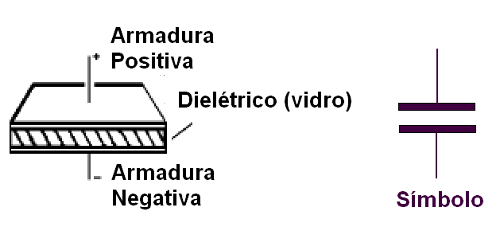
Duas placas, tendo um material isolante entre elas (chamado genericamente dielétrico), manifestam a propriedade de armazenar cargas elétricas e com isso também energia elétrica. Na figura 107 poderemos observar um capacitor em que o dielétrico é uma chapa de vidro e as placas, chamadas armaduras, são placas de metal planas. Dizemos que se trata de um "capacitor plano". Nessa mesma figura temos o símbolo adotado para representar um capacitor.
Quando encostamos uma placa na outra, ou oferecemos um percurso para que as cargas se neutralizem, interligando as armaduras através de um fio, o capacitor se descarrega. Na figura 108 pode-se observar o processo de descarga de um capacitor.
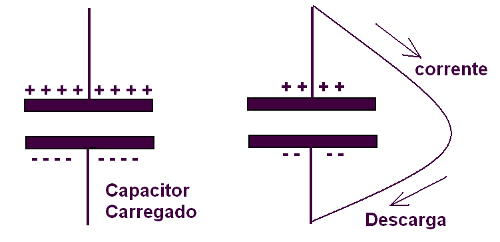
Observe que as cargas ficam armazenadas no capacitor por uma atração eletrostática que ocorre através do seu dielétrico. Assim, entre as armaduras de um capacitor manifesta-se uma tensão elétrica e entre elas existe um campo elétrico uniforme, no caso do capacitor plano.
Também é importante observar que num capacitor carregado sempre temos a mesma quantidade de cargas nas armaduras positiva e negativa.
A capacidade de armazenamento de um capacitor define o que denominamos "capacitância" de um capacitor. Ela depende de três fatores: tamanho das armaduras, material do dielétrico e espessura do dielétrico.
A capacitância ou capacidade de armazenamento do capacitor será tanto maior quanto maiores forem as armaduras, mais fino for o dielétrico e maior for a constante dielétrica do material como dielétrico.
Eletretos
Existe um tipo de material que se comporta como um capacitor natural, sem a necessidade de armaduras. Nesse material, formam-se dipolos elétricos que se orientam de tal forma que de um lado desse material se encontram cargas positivas e do outro as cargas negativas. Podemos dizer que se trata de um “capacitor natural”, conforme mostra a figura 109.
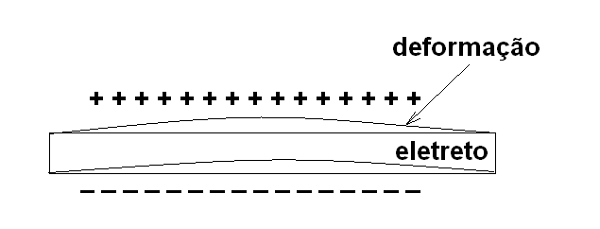
Os eletretos, conforme veremos mais adiante neste curso servem para a fabricação de alguns componentes eletrônicos importantes.
Unidades de Capacitância
A capacidade de um capacitor de armazenar cargas, melhor chamada de capacitância, é medida em Farads (F), mas como se trata de uma unidade muito grande, é comum o uso de seus submúltiplos.
Temos então o microfarad (µF) que equivale à milionésima parte do farad ou 0,000 001 F. Em capacitores muito antigos encontramos o microfarad abreviado como mfd. Um submúltiplo ainda menor é o nanofarad, que equivale a 0,000 000 001 F ou a milésima parte do microfarad e é abreviado por nF.
Finalmente temos o picofarad (pF) que é a milésima parte do nanofarad ou 0,000 000 000 001 F.
Em capacitores muito antigos podemos encontrar o picofarad expresso como mmfd ou micro-microfarad e ainda µµF.
É comum a utilização de potências de 10 para expressar números com muitos zeros. Assim temos as indicações da tabela que demos na lição que trata de resistores.
Veja então que 1 nF equivale a 1 000 pF e que 1 µF equivale a 1000 nF ou 1 000 000 pF.
Tipos de Capacitores
Existem muitos tipos de capacitores, usados nas mais diversas aplicações eletrônicas, conforme o leitor poderá ver na figura 110.
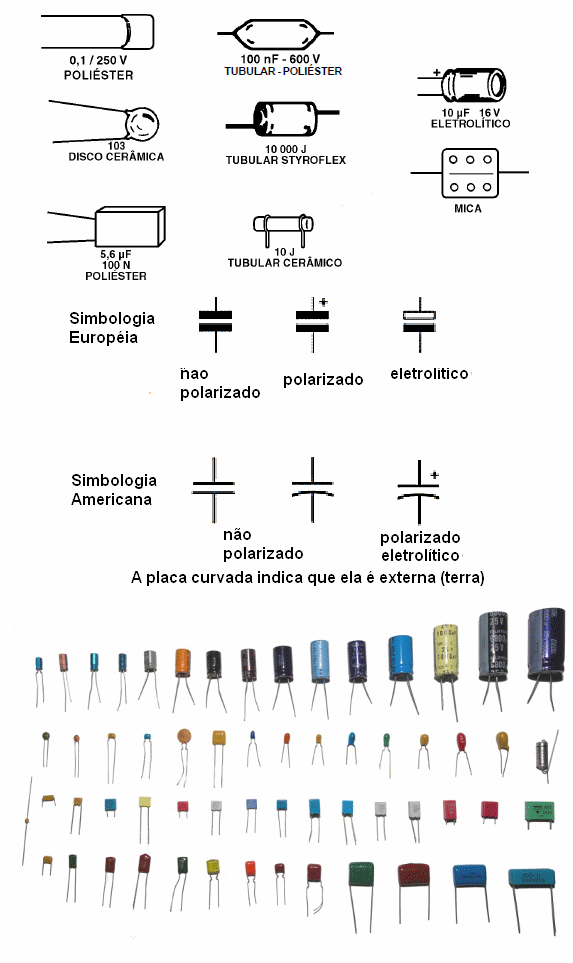
Os capacitores tubulares, que são formados por folhas de condutores e dielétricos enrolados, sendo usados em circuitos de baixas e médias frequências enquanto que os que possuem armaduras e dielétricos planos são usados em circuitos de altas frequências. O porquê será visto em lições futuras.
Observe que os nomes dados aos capacitores dependem justamente do material que é usado como dielétrico ou eventualmente da tecnologia empregada como ocorre no caso dos chamados eletrolíticos.
Um capacitor eletrolítico de alumínio ou simplesmente eletrolítico tem a estrutura básica mostrada na figura 111.
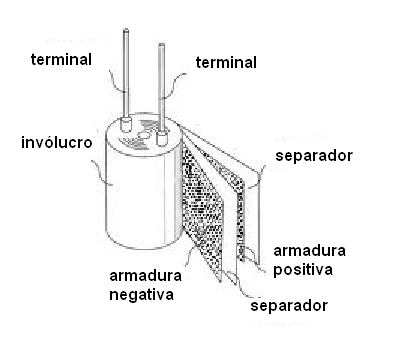
Uma de suas armaduras é de alumínio que, em contacto com uma substância quimicamente ativa, se oxida formando uma finíssima camada de isolante que vai ser o dielétrico. Desta forma, como a capacitância é tanto maior quanto mais fino for o dielétrico, podemos obter capacitâncias muito grandes com um componente relativamente pequeno.
É preciso observar que os capacitores eletrolíticos são componentes polarizados, ou seja, a armadura positiva deve ser sempre a mesma. Se houver uma inversão, tentando-se carregar a armadura positiva com cargas negativas, o dielétrico será destruído e o capacitor inutilizado.
Observando um capacitor deste tipo vemos que sempre existe uma marcação de polaridade (positivo ou negativo) ou algum meio de se fazer essa identificação.
Na família dos capacitores eletrolíticos temos um tipo especial que emprega uma substância que permite obter capacitâncias ainda maiores que as obtidas pelo óxido de alumínio. Trata-se do óxido de tântalo, o que nos leva aos capacitores de tântalo, mostrados na figura 112.

Estes capacitores podem ser encontrados na faixa de 0,1 µF até mais de 100 000 µF.
Super e Hiper Capacitores
A unidade usada para medir a capacitância de um capacitor, o farad (F) é muito grande, assim os capacitores que encontramos nas aplicações práticas têm capacitâncias sempre de frações de farads (microfarads, nanofarads e picofarads).
Segundo pode-se calcular, um capacitor que use as tecnologias comuns para ter uma capacitância de 1 farad deveria ser do tamanho da terra.
No entanto, a tecnologia de fabricação de capacitores com dielétricos cada vez mais finos está possibilitando a fabricação de capacitores pequenos com capacitâncias gigantescas: são os chamados supercapacitores e hipercapacitores, conforme mostra a figura 113.

A carga de tais capacitores representa uma quantidade de energia tão grande que eles podem ser usados como fonte de energia, substituindo pilhas em algumas aplicações.
Energia Armazenada
As cargas armazenadas num capacitor representam energia. Assim, um capacitor armazena energia elétrica. Essa energia não está propriamente nas cargas, mas sim no campo elétrico que se manifesta entre as armaduras. Se pegarmos um capacitor carregado e ligarmos através de um fio seus terminais (armaduras) veremos que ocorre a descarga com uma corrente de muito curta duração e uma faísca mostrando o envolvimento no processo de certa quantidade de energia, conforme mostra a figura 114.
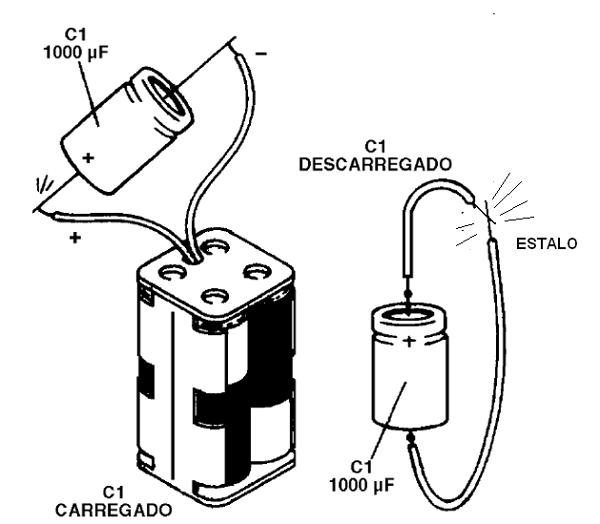
No entanto, a quantidade de energia que um capacitor comum pode armazenar é muito pequena. Mesmo um capacitor de 1 000 uF ligado a uma pequena lâmpada ou LED não os mantém acesos por mais do que alguns segundos.
A energia armazenada num capacitor é medida em Joules (J). Podemos calcular esta energia através da fórmula:
E = ½ x C x V2
Onde:
E é energia armazenada em joules (J)
C é a capacitância em farads (F)
V é a tensão em volts (V)
Veja que a energia é proporcional ao quadrado da tensão, assim se dobrarmos a tensão, a capacidade de armazenamento de um capacitor ficará quadruplicada.
Na prática uma das aplicações para os capacitores de valores elevados (eletrolíticos) é justamente como reservatório de energia. Eles compensam as variações de consumo num circuito descarregando-se quando o circuito exige mais corrente e carregando-se para formar uma reserva quando o consumo é menor. Estudaremos isso no Curso de Eletrônica Analógica.
Códigos de Valores
Alguns tipos de capacitores são muito pequenos, o que dificulta a marcação direta de seus valores e outras características importantes, como a tensão de trabalho e a tolerância.
A tensão de trabalho nos diz qual é a máxima tensão com que um capacitor pode ser carregado sem que ocorra um faiscamento entre as armaduras, rompendo o dielétrico e estragando-o. Essa tensão pode variar entre alguns volts até milhares de volts, dependendo do tipo.
A tolerância nos diz qual é a diferença que podemos encontrar entre o valor real do capacitor e o valor marcado, sem que isso signifique que ele tenha problemas. Assim, para alguns tipos de capacitores também existem códigos especiais para especificação de valores.
Os capacitores cerâmicos de disco, conforme pode ser visto na figura 115, por exemplo, possuem dois tipos de códigos de especificações que não devem ser confundidos.
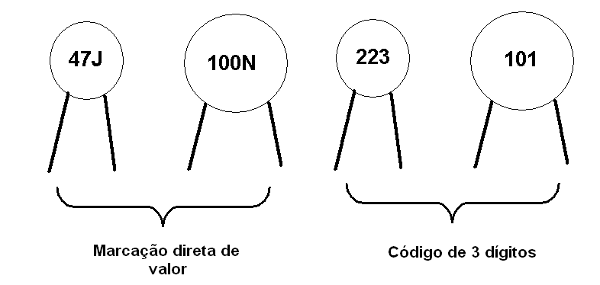
Para os pequenos valores, temos a especificação direta em picofarads (pF) onde existe uma última letra maiúscula que indica a sua tolerância, ou seja, a variação que pode haver entre o valor real e o valor indicado.
Essas letras, com seus significados são:
F = 1%
J = 5%
M = 20%
H = 2,5%
K = 10%
Observe que o “K” é maiúsculo, nesse caso, não deve ser confundido com o “k” minúsculo que indica quilo ou x 1 000.
Assim, 47J significa 47 pF com 5% de tolerância e 47k significa 47 000 pF ou 47 nF!
Para os valores acima de 100 pF, o mais comum é o código de 3 dígitos, conforme o leitor observou na própria figura 115.
Nesse código, multiplicamos os dois primeiros algarismos pelo fator dado pelo terceiro. Por exemplo, se tivermos um capacitor com a indicação 104: Temos que acrescentar 4 zeros ao 10 obtendo 10 0000 pF ou então 10 por 10 000 = 100 000 pF o que é a mesma coisa. Convertendo para nF temos 100 nF ou ainda 0,1 uF. Assim, 104 que resulta em 100 000 pF é o mesmo que 100 nF, ou 0,1 uF.
Para os capacitores cerâmicos temos também a marcação direta, conforme mostra a figura 116 em que os valores são dados em microfarads (µF).
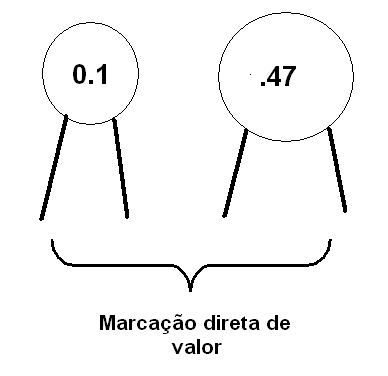
Para obter o equivalente em nanofarads basta multiplicar por 1 000: assim 0,1 µF equivale a 100 nF. Para os pequenos capacitores do tipo SMD, o código é o mesmo usado no caso dos resistores: 3 dígitos. Na figura 117 temos exemplos desses capacitores.

Em alguns casos, o leitor pode ficar confuso se um código de tolerância for acrescentado a essa marcação. Por exemplo, um capacitor com a marcação 223J é um capacitor de 22 nF (22 + 000 pF) com +/- 5% de tolerância. A tabela com o código de tolerâncias é dada a seguir.
| Letra | Tolerância |
| B | +/- 0.10% |
| C | +/- 0.25% |
| D | +/- 0.5% |
| E | +/- 0.5% |
| F | +/- 1% |
| G | +/- 2% |
| H | +/- 3% |
| J | +/- 5% |
| K | +/- 10% |
| M | +/- 20% |
| N | +/- 0.05% |
| P | +100% ,-0% |
| Z | +80%, -20% |
Um código que causa alguma confusão é o formato por letra – número - letra, como Z5U. Um capacitor com a marcação 103 Z5U é um capacitor de 10 000 pF ou 10 nF indicado para temperaturas na faixa de -10° Ca +85° C e uma tolerância de +22% e -56%. A tabela abaixo mostra como ler esse código adicional.
Código do Dielétrico
Primeiro símbolo (letra)Limite inferior de temperaturaSegundo símbolo (numero)Limite superior de temperaturaTerceiro Símbolo (letra)Variação máxima de capacitância na faixa de temperaturasZ+10° C2+45° CA+1.0%Y-30° C4+65° CB+/- 1.5%X-55° C5+85° CC+/- 2.2%--6+105° CD+/- 3.3%--7+125° CE+/- 4.7%----F+/- 7.5%----P+/- 10.0%----R+/- 15.0%----S+/- 22.0%----T+22%, -33%----U+22%, -56%----V+22%, -82%
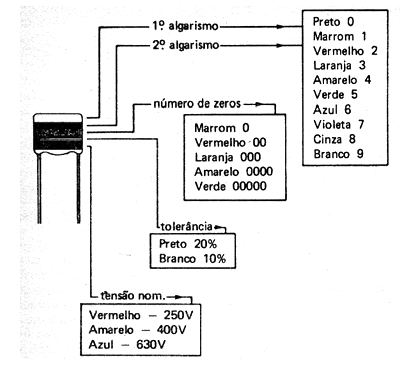
Capacitores antigos como da série “zebrinha” que ainda podem ser encontrados em equipamentos mais antigos, usam um código de faixas coloridas. Nesses capacitores a leitura é feita como no caso de resistores, sendo a quarta faixa a tensão de trabalho e a última faixa a tolerância onde: marrom significa 1% e vermelho 2%, preto 20% e branco 10%.
Existem ainda outros padrões que podem eventualmente se usados na marcação de capacitores.
No entanto, temos um problema interessante a ser considerado: um resistor e um capacitor SMD têm exatamente a mesma aparência e usam o mesmo tipo de código. Só podemos saber se temos um capacitor ou um resistor consultando o esquema do aparelho onde ele está ou fazendo sua medida, ou ainda se formos informados de que componente se trata.
Capacitores SMD
Os códigos básicos dos capacitores SMD (para montagem em superfície) são formados normalmente por duas letras em um dígito. A primeira letra representa o fabricante enquanto a segunda letra representa a mantissa do valor da capacitância. O terceiro símbolo, que é o dígito representa o multiplicador ou expoente em picofarads (pF). Por exemplo, KJ2 é um capacitor de um fabricante desconhecido “K”, que tem 2,2 (J) x 100 = 220 pF.
A tabela abaixo fornece a relação de mantissas para os valores mais comuns:
LetraMantissaLetraMantissaLetraMantissaLetraMantissaA1.0J2.2S4.7a2.5B1.1K2.4T5.1b3.5C1.2L2.7U5.6d4.0D1.3M3.0V6.2e4.5E1.5N3.3W6.8f5.0F1.6P3.6X7.5m6.0G1.8Q3.9Y8.2n7.0H2.0R4.3Z9.1t8.0------y9.0
Os capacitores eletrolíticos SMD também possuem um código especial de marcação de valores que é dado a seguir:
Esses capacitores, apesar de suas reduzidas dimensões, através de código têm marcada tanto a capacitância como a tensão de trabalho. Como exemplo podemos ter 22 6V que consiste num capacitor de 22 uF x 6 V.
No entanto, também pode ser usado um código especial formado de uma letra e 3 dígitos. A letra indica a tensão de trabalho e os três dígitos consistem no valor, sendo os dois primeiros dígitos o valor e o terceiro o multiplicador. O valor obtido é dado em pF. A faixa indica o terminal positivo.
A tabela abaixo dá os valores de tensão para a letra:
| Letra | Tensão |
| E | 2.5 |
| G | 4 |
| J | 6.3 |
| A | 10 |
| C | 16 |
| D | 20 |
| E | 25 |
| V | 35 |
| H | 50 |
Exemplo: C225 significa um capacitor de 2,2 uF x 16 V já que:
225 = 22 x 105 pF = 2,2 x 106 pF = 2,2 uF
Códigos Muito Antigos
Em aparelhos muito antigos, que usam capacitores de mica e cerâmica, podemos encontrar marcações que utilizam códigos de cores na forma de pontos pintados no corpo do próprio componente. A figura 118 mostra alguns desses capacitores.
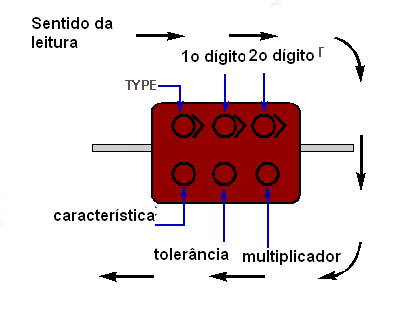
A seta indica o sentido da leitura e a sequência das cores dos pontos é feita da maneira indicada na figura.
Outro tipo de capacitor raro é o pin-up que tem a codificação mostrada na figura 119.
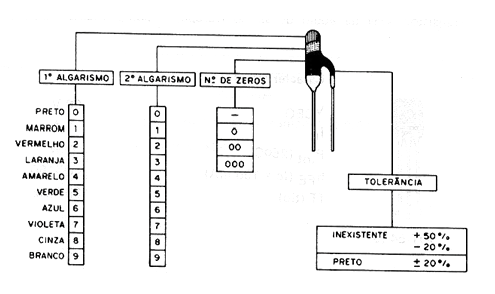
Na figura 120 temos também um outro tipo de capacitor de poliéster que pode ser encontrado em aparelhos antigos com o seu código de leitura. Estes são os capacitores denominados “zebrinha”;
Associação de Capacitores
Da mesma forma que no caso dos resistores, podemos interligar os capacitores de várias maneiras para combinar os efeitos. Analisemos o que ocorre nos dois casos principais.
Capacitores em Paralelo
Na figura 121 temos o modo de associar capacitores em paralelo. Observe a semelhança com a associação de resistores que estudamos na lição passada. Um capacitor está ao lado do outro com seus terminais ligados a um mesmo ponto.
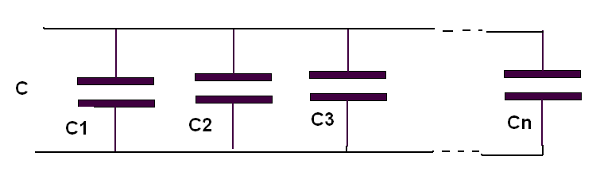
A capacitância equivalente apresenta por uma associação desse tipo é dada pela soma das capacitâncias dos capacitores associados, ou escrevendo isso através de uma fórmula:
C = C1 + C2 + C3 + .........+ Cn (f5.1)
Onde:
C é a capacitância equivalente
C1, C2, C3....Cn são as capacitâncias associadas
As unidades usadas devem ser sempre as mesmas. Por exemplo, se as capacitâncias associadas forem expressas em nanofarads, a capacitância equivalente será encontrada em nanofarads também.
Na figura 122, C1 e C2 estão ligados em paralelo.
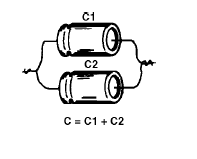
Propriedades da Associação Paralelo de Capacitores:
1. Todos os capacitores ficam submetidos à mesma tensão
2. O maior capacitor se carrega com a maior carga
3. A capacitância equivalente é maior do que o maior capacitor associado
Capacitores em série
Na figura 123 temos o modo de associar capacitores em série. Observe que neste caso, também temos semelhança com a associação de resistores.
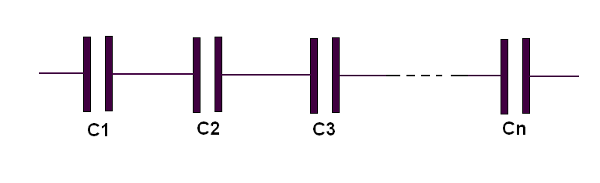
A capacitância equivalente a uma associação desse tipo é dada pela seguinte fórmula:
1/C = 1/C1 + 1/C2 + 1/C3 + ...... + 1/Cn (f5.2)
Onde:
C é a capacitância equivalente
C1, C2, C3 .... Cn são as capacitâncias associadas
Nesse caso também devemos manter a uniformidade das unidades usadas que devem ser as mesmas.
Propriedades da associação série de capacitores:
4. Todos os capacitores ficam carregados com a mesma carga
5. O menor capacitor fica submetido à maior tensão
6. A capacitância equivalente é menor do que a capacitância do menor capacitor associado
Na prática, podemos encontrar capacitores associados em alguns pontos dos aparelhos eletrônicos, mas isso é raro. Saber que podemos associar capacitores para obter maior ou menor capacitância, ou ainda um valor diferente, é importante quando não temos um capacitor do valor desejado e ligamos dois ou mais de certa forma a obter este valor desejado.
No trabalho de manutenção o profissional, diante de um equipamento inoperante, pode improvisar um capacitor de valor que ele não possui associando outros de valores tais que resultem na capacitância desejada.
Outro ponto importante a ser considerado é que nas placas de qualquer equipamento eletrônico, encontramos capacitores de todos os tipos estudados, de acordo com sua função e valor.
Assim, nas fontes e alguns circuitos de alta potência se destacam os eletrolíticos de valores elevados e nas placas mãe de computadores, aparelhos de medida e de controle podemos encontrar os tipos de tântalo e cerâmicos e poliéster em predominância.

Capacitores Variáveis e Ajustáveis
Como no caso dos resistores, também encontramos capacitores cuja capacitância pode ser modificada através de algum tipo de elemento de atuação. Esses capacitores são denominados variáveis ou ajustáveis.
Os capacitores variáveis são aqueles que, através de um sistema de atuação mecânica podemos modificar sua capacitância a qualquer momento por um botão, por exemplo. Um exemplo de capacitor variável é o que encontramos em rádios comuns (não digitais) em que a mudança de estações é feita girando-se um botão.
Os capacitores ajustáveis são aqueles que ficam no interior do equipamento e cuja capacitância é ajustada através de uma chave de fendas comum ou especial. Um exemplo de capacitor ajustável é o trimmer.
Os trimmers são capacitores de ajuste com valores pequenos, normalmente de alguns picofarads. São especificados pela faixa de valores que podem adquirir. Um trimmer de 2-20 pF é um trimmer que pode ter sua capacitância ajustada entre estes dois valores.
Veja figura 124 para os tipos de capacitores juntamente com seus símbolos.
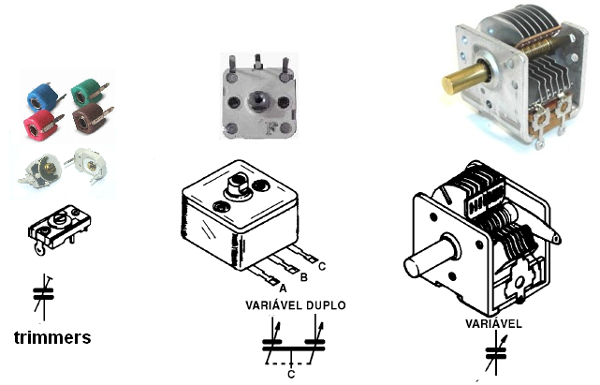
Observe que alguns tipos de capacitores possuem diversas secções como, por exemplo, os encontrados em muitos rádios AM/FM de baixo custo do tipo com sintonia feita por botão.
Capacitores de Estado Sólido
Conforme o leitor vai aprender no Curso de Eletrônica Analógica, existem componentes especiais feitos de materiais semicondutores que se comportam como capacitores. Dizemos que se trata de capacitores de estado sólido ou varicaps e eles são usados nos circuitos de sintonia de muitos aparelhos modernos. Na figura 125 temos o símbolo adotado para representar estes capacitores.
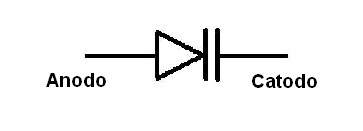
Circuitos de Tempo RC
Quando ligamos um capacitor em série com um resistor temos uma das configurações básicas mais importantes da eletrônica: o circuito de tempo RC (onde R representa o resistor e C o capacitor).
Se ligarmos esse circuito a um gerador (Ve), conforme mostra a figura 126 e acionarmos o interruptor S1, o capacitor não se carrega de imediato, mas numa velocidade que depende de quanta corrente o resistor deixa passar, ou seja, que depende de seu valor.
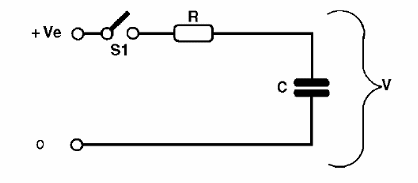
Assim, se fizermos um gráfico que representa a carga do capacitor, teremos uma curva conforme pode ser observado na figura 127.
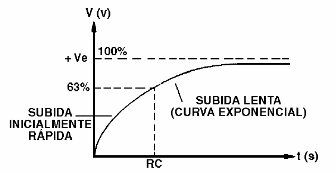
Observe que o capacitor, inicialmente carrega-se rapidamente, pois como está descarregado, a tensão entre suas armaduras é nula e assim pode fluir a corrente máxima que é determinada apenas pelo valor do resistor.
No entanto, à medida que o capacitor se carrega e a tensão entre suas armaduras aumenta, diminui a corrente pelo resistor e a carga vai se tornando mais lenta. A curva tem tal forma que teoricamente o capacitor nunca se carrega totalmente, ou seja, a curva tangencia o valor máximo da carga no infinito.
No entanto, podemos estabelecer um ponto muito importante dessa curva: o ponto em que a carga se torna 63.2% do máximo, mostrado na figura 120.
Esse ponto determina a constante de tempo do circuito, ou seja, pode ser calculado simplesmente multiplicando-se o valor de R pelo valor de C, conforme a seguinte fórmula:
? = R.C
Onde:
? é a constante de tempo em segundos (s)
R é a resistência em ohms (?)
C é a capacitância em farads (F)
Veja que, se depois de carregado um capacitor, o descarregarmos através do circuito que pode ser visto ao na figura 128, também temos uma curva de descarga semelhante.
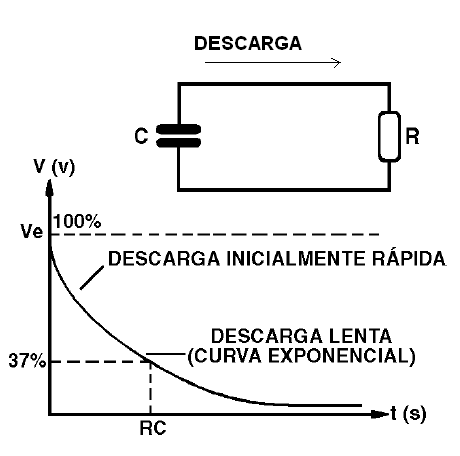
Nessa curva, o ponto que determina a constante de tempo é dado pelo instante em que a carga do capacitor se reduz a 37,8% da carga total, valendo a mesma fórmula.
Blindagens
Dois problemas importantes podem ocorrer em alguns equipamentos: irradiação de interferências e ruídos; recepção de interferências e ruídos. As interferências e ruídos entram e saem dos equipamentos de duas formas: pelos cabos que fazem as conexões a esses equipamentos ou pelo espaço, na forma de campos, conforme mostra a figura 129.
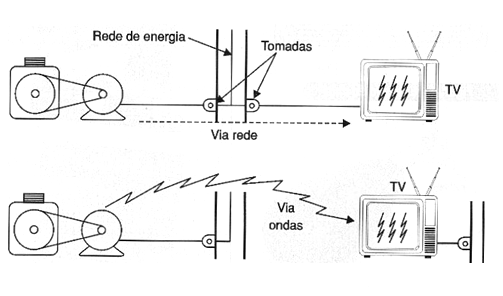
Para evitar que interferências e ruídos sejam irradiados ou recebidos pelos circuitos são usadas blindagens. Basicamente temos dois tipos de blindagens a serem estudadas:
Eletrostática
A blindagem eletrostática mais conhecida é a que se baseia no princípio da gaiola de Faraday. Se envolvermos um corpo por uma gaiola ou blindagem metálica, conforme mostra a figura 130, o campo elétrico no seu interior será nulo, ou seja, não há penetração das linhas de força desse campo.
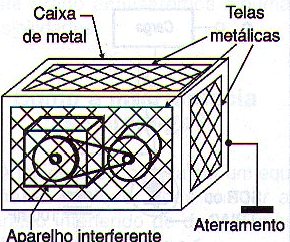
No caso dos circuitos eletrônicos, para que a gaiola funcione, evitando que interferências e ruídos cheguem aos pontos sensíveis, deve haver um aterramento. As blindagens de componentes sensíveis, fios e cabos, se baseiam nesse princípio e é fundamental que as malhas ou as blindagens sejam aterradas, para que operem satisfatoriamente.
Magnética
Existem componentes que, conforme veremos oportunamente produzem fortes campos magnéticos quando funcionam. Além dos motores, solenoides e outros que estudaremos ainda podemos citar os transformadores. Os campos magnéticos desses componentes podem causar problemas de funcionamento em circuitos sensíveis.
A blindagem magnética pode ser feita com determinados materiais, como o cobre e o alumínio, que possuem propriedades diamagnéticas, ou seja, em lugar de concentrar as linhas de força do campo magnético, as dispersam.
Assim, a blindagem desses componentes magnéticos ou de circuitos que sejam sensíveis aos campos magnéticos pode ser feita com esses materiais.
Capacitâncias Parasitas
Dois condutores quaisquer separados por um material isolante formam um capacitor e por isso apresentam uma série de propriedades que caracterizam esses componentes. Isso significa que não é preciso termos realmente uma estrutura montada com duas placas e um material isolante cortado de determinada forma para que um capacitor seja formado.
Dois fios que corram, um lado do outro, dois contactos separados (desligados), duas trilhas de uma placa de circuito impresso, uma área cobreada de uma placa de circuito impresso em uma face e uma outra área do outro lado, formam um capacitor, conforme mostra a figura 131.
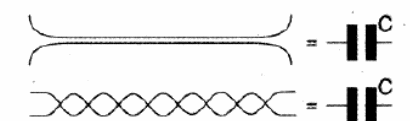
Como esses capacitores aparecem de uma forma até indesejável em alguns casos, podendo influir de forma negativa no funcionamento de um aparelho, dizemos que eles representam "capacitâncias parasitas", ou seja, são capacitores parasitas.
Existem diversas técnicas, que o profissional da eletrônica, principalmente o que vai trabalhar com circuitos rápidos (de comunicações, por exemplo) precisa conhecer para reduzir ou eliminar essas capacitâncias.
Capacitância do Corpo
Quando nos aproximamos de um objeto de metal, sem encostar nele, esse objeto funciona como uma armadura e o nosso corpo outra armadura de um capacitor, cujo dielétrico é o ar que nos separa, conforme mostra a figura 132.
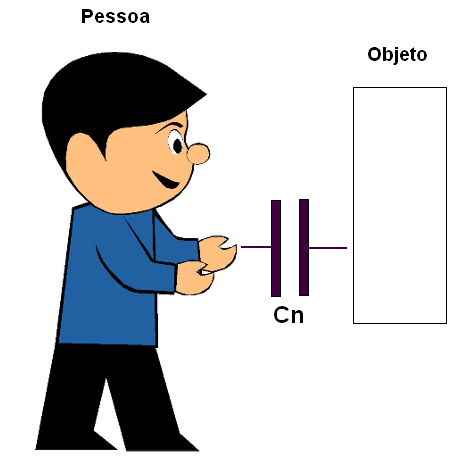
Esse fato pode ser aproveitado em equipamentos eletrônicos para detectar a presença de pessoas. A aproximação da pessoa de uma placa faz com que o circuito ligado a essa placa veja um capacitor cujo valor depende do objeto que se aproxima dele. Quando uma pessoa (ou mesmo um objeto) se aproxima, sua capacitância aumenta e isso pode ser usado para detectar sua presença.
A Terra é um capacitor
Uma esfera metálica carregada de eletricidade é o que denominamos capacitor esférico. Sua capacidade de armazenamento depende de seu diâmetro.
A terra por ser esférica e condutora pode ser considerada um grande capacitor. Os cálculos mostram que sua capacitância é da ordem de 1 Farad.
As lições deste curso são:
Lição 1 – Matéria e energia, a natureza da eletricidade, eletricidade estática
Lição 2 – Energia elétrica, corrente e tensão. O circuito elétrico
Lição 3 – Resistência elétrica, resistores, Lei de Ohm, Lei de Joule
Lição 4 – Tipos de geradores, rendimento e equação do gerador
Lição 5 – Capacitores
Lição 6 – Magnetismo e eletromagnetismo
Lição 9 – Ondas eletromagnéticas