As engrenagens são parte fundamental de qualquer sistema mecânico. Caixas de redução e outros sistemas de transmissão de movimento fazem uso das engrenagens na maior parte dos casos. Veja neste artigo como funcionam as engrenagens e como calculá-las.
MEC291S
Encontramos engrenagens numa infinidade de sistemas que devem transmitir movimento. Um dos casos mais simples está nos antigos batedores de ovos em que um conjunto de engrenagens transmite o movimento circular de uma manivela no plano vertical para o movimento circular de duas peças mecânicas num plano horizontal, conforme mostra a figura 1.

Esse simples dispositivo que faz uso de engrenagens nos mostra que elas podem ser usadas tanto para alterar o tipo de um movimento (aumentando a força ou a velocidade) como também o próprio plano e sentido em que ele é realizado.
Observe pela figura que, enquanto uma das partes do batedor gira num sentido, a outra parte gira no sentido oposto.
Tudo isso nos mostra que as engrenagens podem ser de grande utilidade quando devemos transmitir um movimento contínuo como, por exemplo, de um motor, mudando suas características.
Tipos de Engrenagens
Um sistema de engrenagens não é apenas formado por duas rodas dentadas com diâmetros e portanto números de dentes diferentes. Existem variações que podem ser observadas através da figura 2.
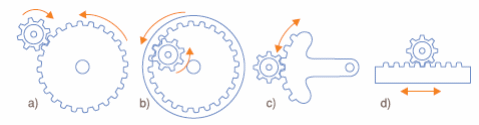
Em (a) temos um sistema comum de engrenagens cilíndricas, do tipo mais usado para redução ou aumento de torque num mesmo plano. No entanto, podemos ter o arranjo mostrado em (b) em que temos um pinhão interno para a transmissão da força. Em (c) temos uma engrenagem tipo setor e em (d) temos um sistema que transmite movimentos lineares.
Como Funcionam
Quando acoplamos duas engrenagens cilíndricas, como as mostradas na figura 3, a alteração do movimento e da força vai depender da relação entre os seus diâmetros.
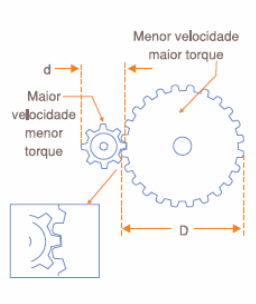
Como para o acoplamento entre as engrenagens é necessário que seus dentes se encaixem perfeitamente, ou seja, sejam iguais, o número de dentes das duas engrenagens estará na mesma relação que os seus diâmetros.
Assim, é o mesmo dizer que duas engrenagens têm uma relação de diâmetros de 10:1 e dizer que possuem uma relação entre dentes de 10:1. Veja que, para que isso seja válido, a relação de diâmetros deve ser tal que nas duas engrenagens encontremos números inteiros de dentes.
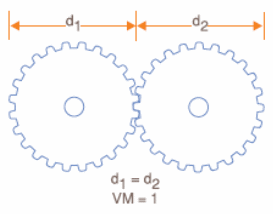
Se as duas engrenagens acopladas tiverem a mesma quantidade de dentes e, portanto o mesmo diâmetro, conforme mostra a figura 4, não obtemos alterações no torque e na velocidade. Apenas o sentido de rotação da engrenagem receptora é contrário daquela que transmite o movimento. Dizemos que este sistema tem uma vantagem mecânica unitária.
Na prática, entretanto, o uso de engrenagens também visa obter algum tipo de vantagem mecânica, ou seja, alterar a força que é transmitida, de modo a se obter mais força e menor velocidade oui vice-versa.
Quando obtemos mais força e menor velocidade, dizemos que o sistema tem uma vantagem mecânica maior que 1 (>1). Por outro lado, se obtemos menos força, mas maior velocidade, o sistema tem uma vantagem mecânica menor que 1 (<1).
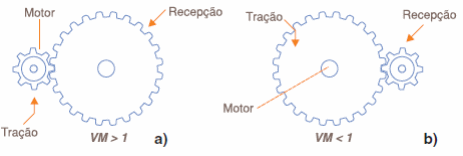
Para obtemos vantagem mecânica maior que 1, a engrenagem que transmite o movimento deve ter menos dentes do que a que recebe, conforme mostra a figura 5(a). Por outro lado, para obtermos vantagem mecânica menor que 1, a engrenagem que transmite o movimento deve ter mais dentes do que aquela que recebe, conforme mostra a figura 5 (b).
Podemos facilmente calcular as características de um sistema formado por duas engrenagens como as indicadas pelas seguintes fórmulas:
a) Variação da velocidade
V1/V2 = n2/n1 (linear)
Onde:
V1 é a velocidade tangencial da engrenagem 1
V2 é a velocidade tangencial da engrenagem 2
n1 é o número de dentes da engrenagem 1
n2 é o número de dentes da engrenagem 2
n1/n2 = ω 2/ω 1
Onde:
ω 1 – velocidade angular da engrenagem 1 (rad/s)
ω 2 – velocidade angular da engrenagem 2 (rad/s)
n1, n2 – como na fórmula anterior
b) Vantagem mecânica
TMA = V2/V1 = n1/n2 = ω 2/ω 1
TMA – vantagem mecânica
c) Variação do torque
M1/M2 = n2/n1
Onde:
M1 - torque aplicado na engrenagem 1 (N.m)
M2 – torque obtido na engrenagem 2 (N.m)
n1, n2 – número de dentes das engrenagens
Uma forma de alterarmos os planos de transmissão dos movimentos, consiste em se usar engrenagens cônicas, conforme mostra a figura 6.
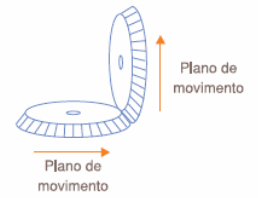
A inclinação dos dentes vai determinar o modo como as engrenagens podem ser acopladas e com isso a alteração nos planos dos movimentos.
Neste caso, também temos alterações das características do movimento transmitido. Valem as mesmas fórmulas do caso anterior.
Caixas de Redução
Nem sempre o uso de apenas duas engrenagens permite obter a vantagem mecânica ou a redução da velocidade e o aumento do torque desejado. Isso ocorre principalmente quando trabalhos com pequenos motores de corrente contínua que são especificados para operarem num regime de alta velocidade e baixo torque.
As velocidades que chegam as 10 000 rpm e os torque da ordem de poucas gramas x cm não se adaptam à maioria das aplicações, principalmente ligadas à mecatrônica, em que precisamos de baixas velocidades (poucas dezenas ou centenas de rpm) e torque elevados (muitos g.cm).
Uma forma de se aumentar o torque e com isso a vantagem mecânica consiste em seu usar diversas engrenagens num arranjo que denominamos “caixa de redução”, conforme mostra a figura 7.
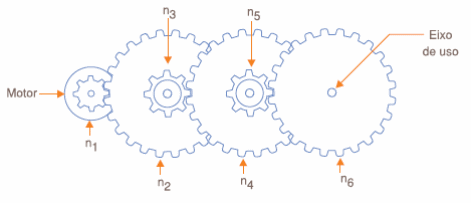
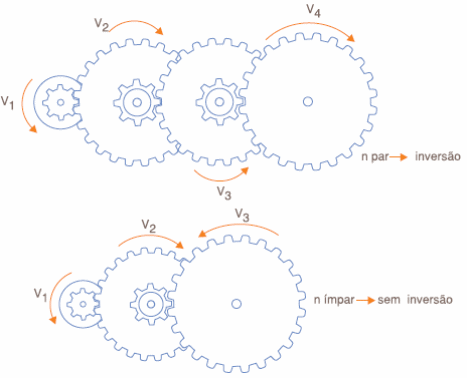
Observe que à medida que vamos acrescentando novas engrenagens temos tanto a alteração do torque como também do sentido do movimento. Com um número par de engrenagens obtemos a inversão do sentido do movimento e com um número ímpar de engrenagens o movimento final tem o mesmo sentido do movimento aplicado, conforme mostra a figura 8.
O cálculo de uma caixa de redução é bastante simples se usarmos apenas engrenagens cilíndricas, conforme mostra o arranjo da figura 9.
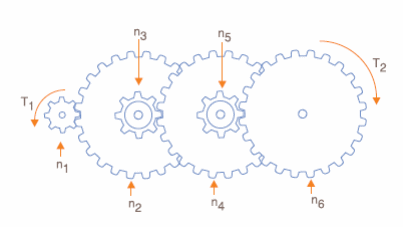
Nessa caixa temos uma verdadeira redução da velocidade, com uma vantagem mecânica maior que (TMA >1).
Nessas condições, consideramos no conjunto as engrenagens pequenas como transmissoras e as engrenagens grandes como receptoras. A relação entre os torques na entrada e saída será dada por:
T1/T2 = (n2 x n4 x n6)/(n1 x n3 x n5)
Onde:
T1 é o torque na entrada (N.m) ou (g.cm)
T2 é o torque obtido na saída (N.m) ou (g.cm)
n2, n4, n6 são os dentes ou diâmetros das engrenagens receptoras (maiores)
n1, n3, n5 são os dentes ou diâmetros das engrenagens transmissoras (menores)
É preciso manter a coerência entre as unidades usadas e lembrar que estamos tratando como se a caixa de redução fosse perfeita, ou seja, não houvesse nenhuma perda por atrito ou outros problemas de resistência mecânica, que na prática podem afetar sensivelmente o torque final obtido.
Lembramos ainda que, sendo os pequenos motores de corrente contínua dispositivos de baixo torque, para vencer a resistência inicial ao movimento, é sempre interessante que o primeiro conjunto de engrenagens tenha uma relação de redução elevada, 10:1 ou maior.
Com uma redução muito baixa, o motor pode travar ou ainda ficar difícil dar a partida no sistema.
Montagem uma Redução
Engrenagens de diversos materiais plásticos podem ser conseguidas em brinquedos, eletrodomésticos e eletroeletrônicos que possuam partes móveis.
Uma redução interessante que pode resultar num interessante trabalho prático para alunos do nível fundamental e médio é a mostrada na figura 10.
Usando uma engrenagem pequena (pinhão) que se encaixe no eixo de um pequeno motor de corrente contínua e uma engrenagem maior que possa ser encaixada no eixo de um carrinho de brinquedo, podemos elaborar um sistema de transmissão experimental para demonstrações.
Esse sistema pode ser acoplado a elevadores, carrinhos, robôs e muitos outros projetos práticos.