O teorema de Fourier diz que sempre é possível selecionar números de a1 a na ia serie mostrada a seguir e ?1, ?2, até ?n de tal forma que qualquer função periódica ou vibração tendo a frequência f (?t) pode ser representada na forma de uma soma de funções ou vibrações harmônicas.
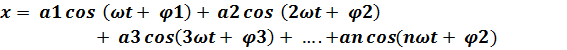
Onde:
x é a amplitude instantânea da forma de onda ou da função (unidade conforme a grandeza)
a1, a2, até na são as amplitudes das harmônica
ω1, ω2, ω3, ωn são os sobretons ou frequências das harmônicas
φ1, φ2, φ3, φn são os ângulos de fase das harmônicas
Nas tabelas seguintes daremos a composição harmônica de formas de onda comuns determinadas pela transformada de Fourier. A porcentagem correspondente também é dada para cada componente (harmônica) tornando os cálculos mais simples.
Tabela 1 – Composição harmônica para sinais quadrados
| Harmônica | Amplitude relativa | Amplitude porcentual |
| Fundamental | (4/Π)*V | 127 |
| 2º | 0 | 0 |
| 3º | (4/3Π)*V | 42,5 |
| 4º | 0 | 0 |
| 5º | (4/5Π)*V | 25,5 |
| 6º | 0 | 0 |
| 7º | (4/7Π)*V | 18,2 |
Tabela 2 – Composição harmônica para sinais triangulares
| Harmônica | Amplitude relativa | Amplitude porcentual |
| Fundamental | (8/Π2)*V | 81 |
| 2º | 0 | 0 |
| 3º | (8/9Π2)*V | 9 |
| 4º | 0 | 0 |
| 5º | (8/25Π2)*V | 3,2 |
| 6º | 0 | 0 |
| 7º | 8/(49Π2V) | 1,6 |
Tabela 3 – Composição harmônica para sinais dente de serra
| Harmônica | Amplitude relativa | Amplitude porcentual |
| Fundamental | (1/n)*V | 31,8 |
| 2º | (2/3Π) *V | 21,2 |
| 3º | 0 | 0 |
| 4º | (2/15Π) * V | 4,2 |
| 5º | 0 | 0 |
| 6º | (2/35Π) *V | 1,8 |
| 7º | 0 | 0 |
Tabela 4 - Composição harmônica para o retificador de onda completa
| Harmônica | Amplitude relativa | Amplitude porcentual |
| Fundamental | (3/Π)*V | 63,6 |
| 2º | (4/3Π)*V | 42,3 |
| 3º | 0 | 0 |
| 4º | 4/15Π | 8,5 |
| 5º | 0 | 0 |
| 6º | (4/35Π)*V | 3,6 |
| 7º | 0 | 0 |