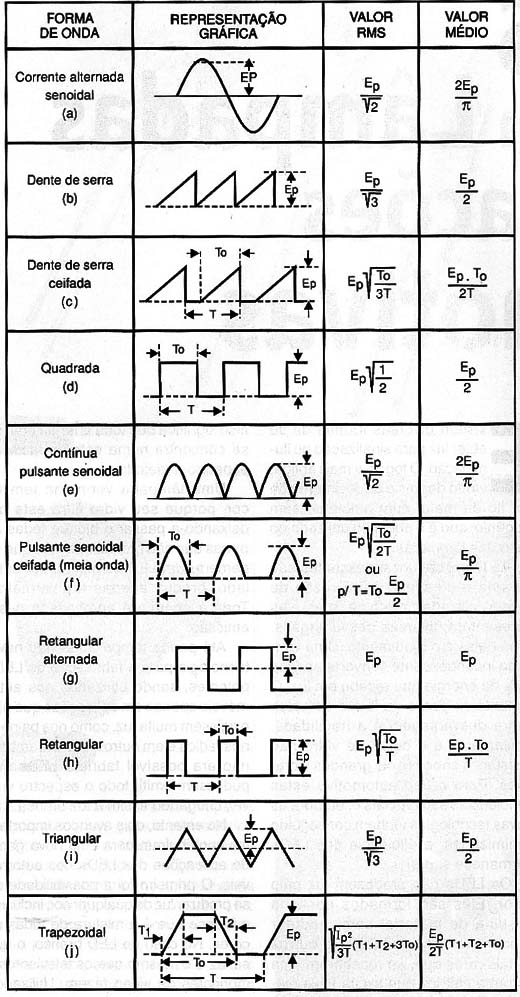
Os valores médio e RMS (root mean square) de um sinal dependem de sua forma de onda. Para os sinais senoidais a maioria dos leitores têm os valores memorizados, mas quando se trata de outras formas de onde, a disponibilidade de informação adicional pode ser importante para um projeto evitando cálculos trabalhosos.
O valor médio de uma tensão ou qualquer outro tipo de sinal (potência ou corrente) depende da forma de onda deste sinal havendo processos de cálculos definidos para cada caso.
Para o valor médio quadrático ou RMS (Root Mean Square) leva-se em conta a equivalência com um sinal contínuo enquanto que para o valor médio o que se faz é tirar a média aritmética dos valores instantâneos.
Os resultados são diferentes e com isso os efeitos físicos.
Na tabela abaixo analisamos os principais casos de formas de ondas comuns nos aparelhos eletrônicos.
Assim, em (a) temos uma corrente alternada senoidal com um valor de pico igual a Ep (tensão de pico). Evidentemente, os mesmos resultados podem ser aplicados à potências e correntes de pico.
Em (b) temos uma forma de onda dente de serra com valor de pico igual a Ep.
Para o sinal dente de serra mostrado em (c) temos um período ativo To que deve ser considerado em relação ao tempo total do ciclo. O valor de pico é Ep neste caso.
Em (d) temos um sinal retangular com ciclo ativo de 50%.
Para um sinal que corresponda a retificação de uma tensão senoidal em onda completa temos as fórmulas mostrada em (e).
Se a retificação for de meia onda temos as fórmulas válidas em (f).
Em (g) temos o caso em que a tensão ou sinal retangular é alternado com um valor de pico igual a Ep.
Para um sinal retangular com ciclo ativo diferente de 50% temos as fórmulas mostrada em (h).
Finalmente em (i) temos as fórmulas para o caso de um sinal triangular alternado.
Um sinal trapezoidal com os diversos tempos envolvidos (tempo de subida (T1), temo de descida (T2), tempo ativo (To) e tempo total (T) é mostrado em (j) com as formulas usadas para se calcular o valor de pico e rms.