Eletrônica de Potência
Quando falamos em eletrônica de potência nos referimos aos circuitos e dispositivos que operam com correntes intensas e eventualmente tensões elevadas, resultando disso o manuseio de potências elevadas.
Como estes circuitos e dispositivos normalmente são encontrados nas indústrias, no controle de máquinas pesadas e outros automatismos, é comum que este ramo da eletrônica também seja tratado como Eletrônica Industrial, Automação Industrial, ou mesmo Mecatrônica.
O termo Mecatrônica deve-se ao fato que na maioria dos casos, os dispositivos e circuitos de potência são usados para controlar equipamentos mecânicos como máquinas industriais, automatismos, veículos, braços robóticos, robôs autônomos, etc.
Assim, nesse volume deste curso trataremos inicialmente de dispositivos e componentes eletrônicos que operam com correntes intensas e eventualmente tensões elevadas, manuseando altas potências.
Num volume posterior trataremos dos circuitos que fazem isso como os inversores de potência, controles de potência, disjuntores, circuitos de proteção e muitos outros.
Observamos ainda que muitos dos dispositivos que abordaremos não manuseiam por si altas potências, mas são utilizados no controle de dispositivos de altas potências, daí ser importante sua inclusão nos nossos estudos.
Neste grupo enquadram-se pequenos dispositivos como os diacs, SIDACs SUS, SBS, TVS, etc.
Lembramos finalmente que os conceitos básicos utilizados neste livro foram estudados nos volumes anteriores desta série, em especial o Curso de Eletrônica – Eletrônica Básica – Vol 1, e Curso de Eletrônica – Eletrônica Analógica – Vol 2 – do mesmo autor.
Unidades Elétricas
Neste item faremos uma pequena revisão das principais unidades elétricas, com destaque à corrente, tensão e potência, cujo conhecimento deve ser muito bem definido, para que não fiquem dúvidas no entendimento do princípio de funcionamento de componentes e circuitos de potência.
Se o leitor tem um conhecimento firme deste assunto, pode saltar este item, indo para o seguinte.
Começamos então por revisar um conceito de vital importância para a eletrônica de potência: a conservação da energia.
Princípio da Conservação da Energia
Um princípio muito importante que frequentemente será lembrado ao estudarmos fenômenos elétricos é o da conservação da energia. Este princípio afirma que a energia não pode ser criada nem destruída, ela sempre se conserva.
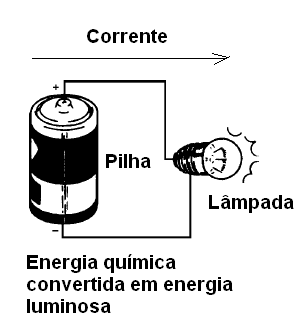
Assim, quando uma pilha alimenta uma lâmpada, a luz produzida tem a mesma quantidade de energia que a pilha gasta para isso. Da mesma forma, se você tem um amplificador, a quantidade de som obtida (energia) é a mesma que a quantidade de energia elétrica que ele consome ao ser ligado na tomada.
Em outras palavras, nos processos que estudaremos envolvendo eletricidade, quantidade de energia presente será sempre a mesma. Ela apenas passará de um tipo para outro, ou seja, se transformará.
Veja na figura 1 um exemplo, em que a energia química liberada no interior da pilha se transforma em energia elétrica que, depois alimenta uma lâmpada se transformando em energia luminosa (luz) e calor (a lâmpada esquenta). Se medirmos a quantidade de luz e calor produzidos pela lâmpada veremos que é exatamente igual à quantidade de energia liberada no processo químico no interior da pilha.
Entendendo as Unidades - Corrente, Tensão e Potência
É um fato inadmissível que muitos profissionais da eletrônica possam confundir grandezas elétricas, como corrente, tensão e potência. Utilizando essas grandezas de forma errada é possível causar problemas sérios de funcionamento de um equipamento ou mesmo comprometer a segurança e o que pode ser muito mais grave: desacredita a competência do profissional ou de qualquer praticante da eletrônica.
Neste item, indicado aos que ainda fazem confusões, procuramos de uma forma simples eliminar as confusões que ainda possam existir.
É comum vermos profissionais utilizar forma completamente errada as grandezas elétricas, confundindo tensão, corrente e potência.
Quem já não ouviu um profissional "competente" dizer que tal aparelho funciona com uma "corrente" de 110 V ou coisa semelhante?
Para um estudante de eletrônica que faça tal afirmação o mínimo que se recomenda é um zero ou um bom castigo!
Mesmo alguns que já não fazem este tipo de citação podem, às vezes, ter dúvidas que demonstram que a confusão relativa à corrente, tensão e também potência persiste em muitos casos.
CORRENTE E TENSÃO
Uma corrente é um fluxo de cargas elétricas.
Elétrons livres que se movem num fio de cobre formam uma corrente elétrica.
A medida dessa corrente é feita em função da quantidade de elétrons ou cargas que passam por um ponto desse fio em cada instante, conforme mostra a figura 2.
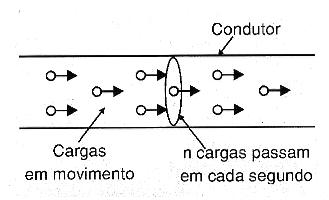
Quanto mais cargas passarem por este ponto, maior é a intensidade da corrente.
Dizemos cargas e não simplesmente elétrons, pois conforme sabemos, a corrente tanto pode ser obtida quando elétrons livres se movimentam num sentido, caso de um metal, como lacunas em sentido oposto como, por exemplo, num semicondutor do tipo P.
Para medir esta corrente a unidade usada é o ampère (A).
Um ampère (1 A) corresponde a uma quantidade de cargas equivalente a 1 Coulomb (1 C) passando por um ponto de um condutor em cada segundo.
Levando em conta que cada elétron (ou lacuna) tem uma carga de 1,6 x10-19 Coulombs, podemos ter uma idéia de quantos elétrons estão se movendo num fio e passando por um certo trecho dele quando uma corrente de 1 A está sendo conduzida.
Se os leitores pensam que a velocidade desses elétrons é muito grande, estão enganados.
É neste ponto que entra então o conceito de tensão.
Como um fluxo de água num encanamento, a eletricidade precisa ser "empurrada" por uma força externa.
A ação externa responsável por isso é justamente a tensão.
Assim, temos diversas formas de expressar essa força externa:
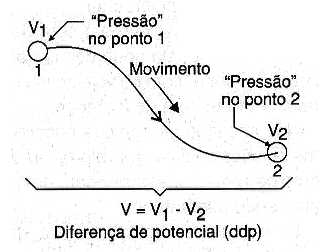
Uma delas é tomarmos como referência a diferença de pressão que existe entre as extremidades de um fio, por onde se estabelece a corrente, conforme mostra a figura 3.
É como se tivermos um reservatório de água a 10 metros de altura e estabelecermos um fluxo de água por um cano com a saída em 5 metros de altura.
A diferença entre os níveis ou pressões da água é 5 metros, conforme mostra a figura 4.
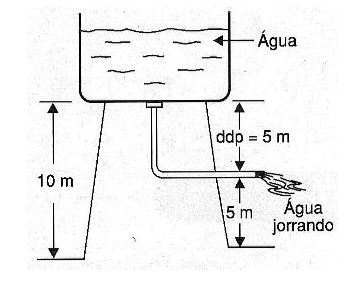
Para a eletricidade podemos ter a caixa de água num "potencial" de 10 volts e a extremidade do fio num "potencial" de 5 volts de modo que a diferença de potencial ou d.d.p. será de 5 volts.
Em outras palavras, podemos indicar como causa para a circulação de uma corrente a diferença de potencial entre as extremidades de um fio ou circuito.
Outra maneira é sempre expressar a pressão que podemos ter num encanamento de água tomando como referência, por exemplo, o nível do mar, conforme mostra a figura 5.
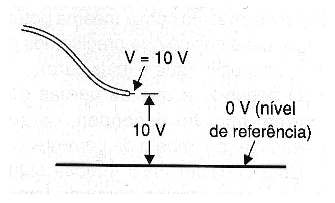
Fazendo assim, não precisaremos saber qual é o potencial em que se encontram cada extremidade do fio.
Podemos simplesmente dizer que o potencial ou tensão no fio é de tantos volts, referindo à força disponível para empurrar a corrente e levando em conta que a outra extremidade se encontra no nível de referência ou zero, conforme mostra a figura 6.
Veja então que enquanto a tensão é a causa do movimento das cargas a corrente é o efeito, ou seja, o movimento dessas cargas.
Sem tensão não há circulação de corrente, se bem que se possa manifestar uma tensão sem haver corrente.
Entre os pólos de uma pilha, por exemplo, manifesta-se uma diferença de potencial, ou seja, existe a possibilidade da pilha aplicar uma tensão num circuito.
No entanto, só haverá corrente no momento em que for ligado aos pólos da pilha um meio ou circuito por onde a corrente possa fluir.
Numa tomada de energia existe uma "tensão" de 110 V, mas corrente só vai existir no momento em que algum aparelho for ligado a esta tomada.
CORRENTE X TENSÃO = POTÊNCIA
Um fato importante que todo o praticante de eletrônica deve ter em mente é que não se pode criar energia a partir do nada. Já vimos isso ao tratar do princípio da conservação da energia.
A energia entregue a um circuito elétrico depende tanto da tensão como da corrente.
É da "força" com que as cargas elétricas são empurradas num fio e da sua quantidade que depende a quantidade de energia que um circuito pode receber em cada instante, ou seja, sua potência elétrica.
Assim, a potência elétrica de um circuito, conforme mostra a figura 7, é dada pelo produto da tensão pela corrente.
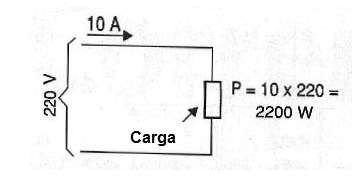
A potência, que é medida em watts (W), é uma característica própria de um circuito e normalmente não pode ser alterada.
No entanto, o modo como essa potência pode ser fornecida ao circuito pode ser modificado.
Assim, se um circuito precisar de 100 watts para funcionar, podemos projetá-lo de tal forma que ele seja alimentado por 20 volts, caso em que a corrente que vai circular no funcionamento normal (desprezando-se as perdas) será de 5 ampères, como podemos projetá-lo para funcionar com 50 volts, caso em que a corrente será de 2 ampères.
Nos circuitos eletrônicos encontramos tensões de diversos valores, assim como correntes que dependem do que está sendo alimentado.
E, na alimentação externa dos circuitos temos também diversas possibilidades.
Um exemplo disso está na nossa própria instalação elétrica.
Se tivermos um chuveiro que deva operar com uma potência de 2 200 watts, o que se considera razoável para dar um bom aquecimento a um fluxo normal de água temos duas possibilidades para alimentá-lo:
Se ligarmos esse chuveiro na rede de 110 V, para obter os 2 200 watts, a corrente que vai circular será de 20 ampères.
Se ligarmos esse mesmo chuveiro na rede de 220 V, a corrente será só de 10 ampères.
Veja que não estamos economizando energia no segundo caso!
Pagamos pelos watts multiplicados pelo tempo em que o chuveiro fica ligado, e nos dois casos a potência é de 2 200 watts.
Então, qual é a vantagem?
Os fios que transportam energia elétrica possuem certa resistência que depende de sua espessura e de seu comprimento.
Da mesma forma, em função da espessura, os fios apresentam certa limitação à intensidade da corrente que podem conduzir.
Assim, se usarmos a rede de 110 volts para transferir energia para um chuveiro e sua instalação usar fios longos temos dois problemas a considerar.
O primeiro ‚ que a corrente deve ser duas vezes maior do que se usarmos 220 volts, mesmo com a mesma potência, o que significa que precisamos de fio mais grosso (que é mais caro).
O segundo é que, as perdas que ocorrem num fio dependem de sua resistência e também da corrente.
Uma corrente mais intensa significa que, num mesmo percurso temos perdas de energia maiores.
Vamos dar um exemplo numérico:
Vamos supor que para o chuveiro que em 110 volts exige uma corrente de 20 ampères, tenhamos de usar um fio que apresente uma resistência de 1 ohm, conforme mostra a figura 8.
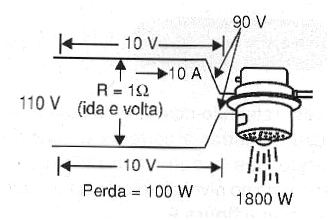
A queda de tensão será dada por:
V = R x I
Onde: V é a queda de tensão no fio, ou seja, a "diminuição" da tensão no circuito em volts.
R é a resistência do fio em ohms
I é a intensidade da corrente em ampères
V = 1 x 20
V = 20 volts
Veja então que, no chuveiro teremos apenas 90 volts em lugar dos 110 aplicados, pois 20 volts "se perdem" nos fios.
A potência que esses 20 volts representam também é preocupante:
P = V x I
Onde:
P é a potência dissipada no fio em watts
V é a queda de tensão no fio em volts
I é a intensidade de corrente em ampères
P = 20 x 20
P = 400 watts
Ora, esses 400 watts perdidos na instalação vão se transformar em calor, aquecendo os fios o que realmente é preocupante!
Se usarmos 220 V no mesmo chuveiro, mesmo com uma instalação que tenha 1 ohm, as coisas mudam:
Lembramos que neste caso, para obter os 2 200 watts a corrente será de 10 ampères.
V = R x I
V = 1 x 10
V = 10 volts
A queda de tensão será de 10 volts apenas, o que quer dizer que em lugar de 220 V no chuveiro, teremos 210 volts.
A potência perdida no fio e dissipada na forma de calor será:
P = V x I
P = 10 x 10
P = 100 watts
As perdas são bem menores, neste caso, e conseqüentemente o aquecimento da instalação.
Este é o motivo pelo qual damos preferência às tensões mais elevadas quando devemos alimentar circuitos de altas potências ou transmitir energia elétrica por meio de fios longos.
Outro caso importante que envolve as duas grandezas, tensão e corrente, ocorre num transformador ou numa fonte de alimentação, conforme mostra a figura 9.
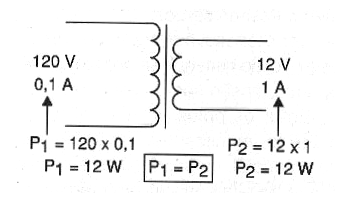
Se a fonte fornece 12 V com corrente máxima de 1 ampère, e na entrada a tensão aplicada é de 120 volts, qual será a corrente que circular pelo circuito de entrada?
Supondo que essa fonte tenha um rendimento próximo de 100% isso significa que a potência do circuito de entrada será a mesma do circuito de saída.
No circuito de saída a potência será:
P = V x I
P = 12 x 1
P = 12 watts
(12 volts sob 1 ampère)
Na entrada teremos a mesma potência: 12 watts.
A corrente será então:
I = P/V
I = 12/120
I = 0,1 A
Veja então que a corrente será de apenas 0,1 A ou 100 mA.
Um fusível de 500 mA pode ser empregado nesta fonte, protegendo o circuito de entrada, mesmo levando-se em conta que sua saída é de 1A.
Potência contínua e alternada
Uma corrente que flui sempre no mesmo sentido e com a mesma intensidade, como ocorre quando ligamos uma lâmpada a uma pilha, é chamada "corrente contínua". Podemos abreviar essa designação por CC ou ainda, usando o termo americano "direct current" por DC. Na figura 10 temos o gráfico que indica a intensidade de uma corrente contínua ao longo do tempo.
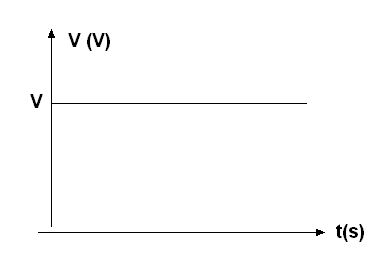
Observe que, para provocar uma corrente contínua precisamos estabelecer em seu circuito uma tensão constante, ou seja, uma tensão que também seja contínua.
No entanto, nas aplicações de potência que fazem uso da energia da rede de distribuição, o tipo de corrente encontrado é outro.
Esta corrente é gerada por alternadores cujo princípio de funcionamento foi analisado no nosso curso de eletrônica analógica (Vol 2). O leitor poderá revisar seu princípio de funcionamento naquela edição do mesmo autor.
Conforme estudamos, na saída de um alternador temos uma corrente que varia entre máximos e mínimos regularmente, ou seja, inverte constantemente de sentido de circulação, o que corresponde a uma corrente alternada.
Vemos então que, se ligarmos um receptor a um gerador desse tipo, metade do tempo de um ciclo, a corrente circula num sentido, e na outra metade ela circula no sentido oposto. A energia da rede pública e utilizada nas indústrias e outras aplicações é desse tipo.
Conforme estudamos anteriormente, podemos representar a corrente gerada por esse tipo de gerador por uma curva chamada senóide, conforme mostra a figura 11.
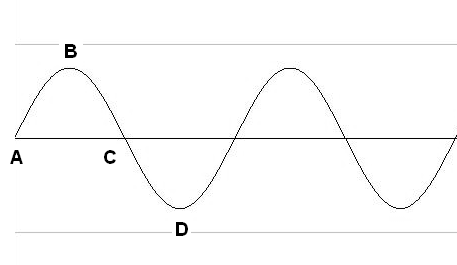
O gerador que produz a energia que consumimos dá 60 voltas por segundo, o que quer dizer que em cada segundo a corrente circula 60 vezes num sentido e 60 vezes no sentido oposto. Dizemos que a corrente da rede pública que alimenta residências, instalações comerciais e industriais e outras é alternada com uma frequência de 60 Hertz (Hz).
Existem países, como a Argentina, em que a corrente gerada tem uma frequência diferente, como 50 Hz. O interessante é que os efeitos obtidos na transmissão de energia usando corrente alternada são os mesmos que seriam obtidos com a corrente contínua, com vantagens que ficarão claras no decorrer do curso. Tomemos o seguinte exemplo:
Passando pelo filamento de uma lâmpada ou por um elemento de aquecimento, os efeitos finais são sempre os mesmos: ao serem empurradas, as cargas transferem energia em forma de calor e ao serem puxadas também, o que quer dizer que as lâmpadas acendem do mesmo jeito e os aquecedores aquecem do mesmo jeito.
Formas de onda, frequência, fase e valores
A representação gráfica de uma corrente alternada tem uma forma muito especial: dizemos que se trata de uma forma de onda "senoidal", conforme estudamos no curso de eletrônica analógica.
Isso nos leva a dizer que a corrente alternada que é distribuída para casas, comércio e indústria é alternada com forma de onda senoidal e frequência de 60 Hz. Analisando essa forma de onda existem diversos valores importantes que o profissional da eletricidade e eletrônica de potência deve conhecer.
O primeiro, de que já falamos, é a frequência que é o número de vezes em cada segundo em que se completa um ciclo da geração dessa energia. A frequência é medida em hertz (Hz). O tempo de duração de um ciclo completo nos dá o período da corrente alternada.
Para uma corrente alternada de 60 Hz, por exemplo, o período ou tempo de um ciclo completo é 1/60 s, conforme mostra a figura 12.
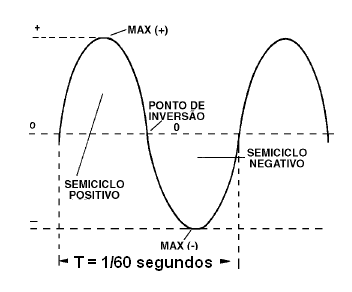
Veja que "o período é o inverso da frequência" ou, escrevendo isso como fórmula:
T = 1 / f
Onde:
T é o período (em segundos)
f é a frequência (em hertz)
A amplitude de uma tensão alternada é expressa de diversas formas, conforme podemos observar pela figura 13.
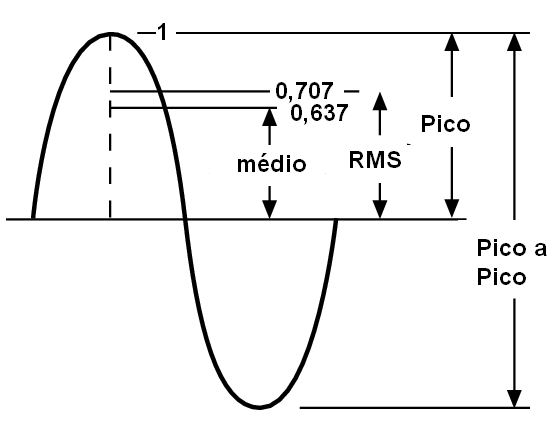
O valor máximo que uma tensão alternada atinge é o valor de pico. Indicamos esse valor por Vp. Metade do valor máximo nos dá o valor médio ou Vm.
No entanto, um valor muito importante é o "valor médio quadrático" ou "root mean square", do inglês, que nos leva a abreviação Vrms. Esse valor corresponde à raiz quadrada de 2 dividida por 2 vezes do valor máximo, ou conforme mostra a fórmula:
Vrms = 0,707 x Vp
Onde:
Vrms é a tensão média quadrática (em volts)
Vp é a tensão de pico
0,707 é a raiz quadrada de 2 (1,41) dividido por 2
Levando em conta que a raiz quadrada de 2 é aproximadamente 1,41, dividindo esse valor por 2, obtemos 0,707. Isso significa que obtemos a tensão rms multiplicando a tensão de pico por 0,707. Da mesma forma, conhecendo a tensão rms obtemos o valor de pico, multiplicando-o por 1,41.
A tensão de "110 V" que encontramos na nossa rede de energia tem esse valor rms. Assim, no instante em que ela se encontra no seu máximo, o pico vai a:
Vp = 1,41 x 110 = 155,1 V
O mesmo é válido para as intensidades de corrente: podemos falar em corrente de pico (Ip), corrente média (Im) e corrente rms (Irms) num circuito.
Outro valor importante que devemos observar na representação de uma tensão ou corrente senoidal é a sua fase. A cada instante, dentro de um ciclo, a tensão alternada tem certo valor. Este valor muda constantemente, dependendo da frequência da tensão alternada.
Em certas aplicações é importante saber o valor que a tensão ou a corrente num circuito de corrente alternada assume num certo instante dentro do ciclo.
Para esta finalidade o que se faz é dividir o ciclo em 360 graus (como numa circunferência) e indicar o instante por um ângulo entre 0 e 360, conforme o leitor poderá constatar pela figura 14.
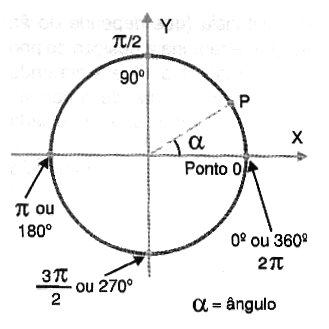
Os 360 graus são adotados lembrando que um ciclo de uma corrente alternada é gerado numa volta completa do alternador. Dessa forma pode-se indicar o instante desejado num ciclo por um ângulo de fase, dado em graus.
Podemos também usar o mesmo conceito para comparar duas correntes ou tensões alternadas que não estejam perfeitamente sincronizadas, ou seja, que não atingem os pontos de máximo e mínimo no mesmo instante.
Dizemos que estas correntes estão "defasadas" e podemos indicar a diferença de fase entre elas por um ângulo, conforme pode ser observando se na figura 15.
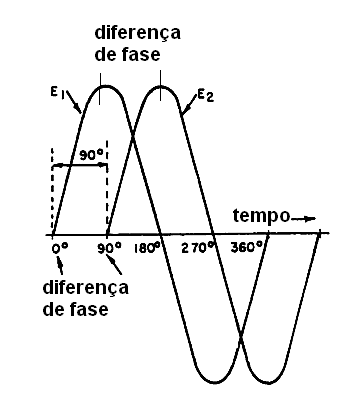
Estes conceitos são muito importantes em eletrônica de potência.
Alternadores
Os alternadores são geradores que convertem energia mecânica em energia elétrica. No caso específico desses geradores, a energia se torna disponível na forma de correntes alternadas. Encontramos os alternadores em diversas aplicações como, por exemplo, nas usinas hidroelétricas e nos automóveis.
Nas usinas são produzidas grandes quantidades de energia a partir da força das águas represadas, do vento ou mesmo do vapor (usinas termoelétricas), enquanto que no automóvel, aproveita-se a força do motor.
Tanto nas usinas como nos alternadores dos automóveis temos basicamente dois conjuntos de bobinas. Um conjunto rotor que gira para cortar as linhas de força do campo magnético e um conjunto estator que cria o campo magnético, mas não se movimenta.
Energia bifásica e trifásica
A energia que recebemos em nossa casa vem na forma de uma tensão alternada que depende da configuração da rede.
Num primeiro caso temos a configuração em triângulo de 220 V em que entre cada fase a tensão é de 220 V e entre o neutro e a fase a tensão é de 110 V com uma configuração em estrela. A figura 16 mostra o que ocorre.
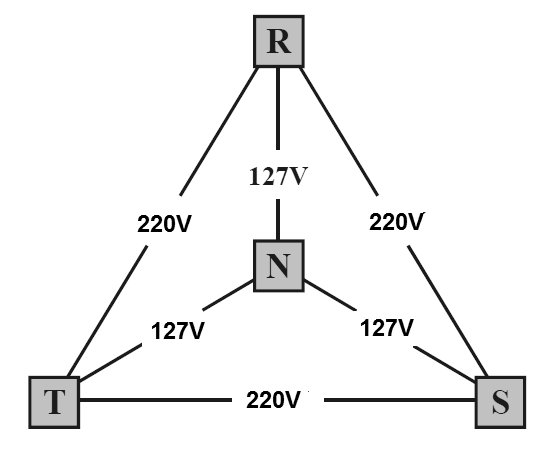
Observe que apesar da soma das tensões de fase e neutro ser de 254 V, e não 220 V, os valores devem considerar as diferenças de fase de 120 graus.
Num segundo caso temos a rede em 380 V, em que a tensão entre fases é de 380 V, com a configuração em triângulo, e entre cada fase e o neutro temos 220 V, na configuração estrela, mostrada na figura 17.
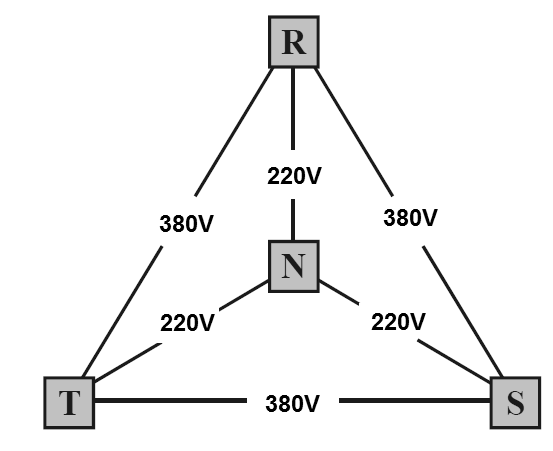
Nas aplicações industriais e de potência a energia é disponibilizada na forma trifásica. Essa forma de se gerar e distribuir energia em sistemas de corrente alternada é empregada principalmente na indústria, por motivos diversos como, por exemplo, a maior conveniência na alimentação de motores elétricos de alta potência.
Nesse sistemas são geradas três tensões com diferenças de fase de 120 graus, conforme mostra a figura 18.
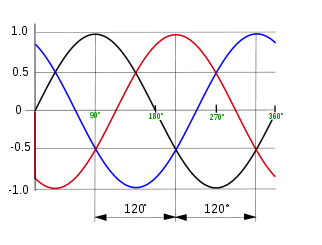
O que se faz para isso é utilizar um sistema gerador em que temos três tensões alternadas disponíveis em bobinas diferentes, conforme mostra a figura 19.
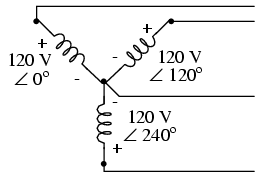
Cada uma das bobinas, que tem uma extremidade ligada a um pólo neutro comum, entrega uma tensão senoidal levemente defasada em relação à outra.
Potência Ativa e Potência reativa
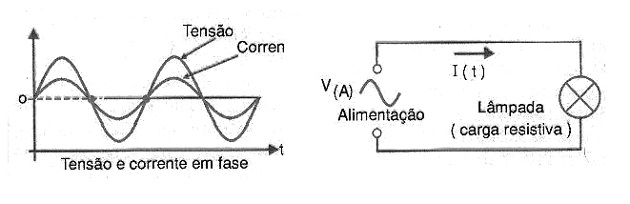
Potência ativa é a que efetivamente realiza um trabalho sendo convertida totalmente em luz, calor, movimento, etc. Essa potência é medida em W (watt) e seus múltiplos (kW ou MW).
Um exemplo de carga que consome totalmente a potência que lhe é fornecida é uma lâmpada incandescente. Ela representa uma carga resistiva pura (ôhmica), conforme mostra a figura 20, pois nela corrente e tensão estão em fase.
No entanto, em muitas aplicações encontramos cargas que não são resistivas puras, mas sim reativas (capacitores e indutores) como é o caso de motores.
Numa carga deste tipo, a potência é reativa e é medida em VAR (Volt-Ampères Reativos) ou seus múltiplos (kVAR e MVAR), conforme mostra a figura 21.
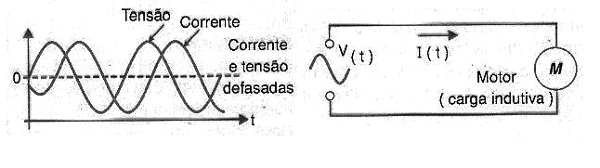
O que ocorre é que nos indutores, a potência reativa não é usada na produção de trabalho, pois ela apenas tem por função estabelecer os campos magnéticos.
Essa potência, não aproveitada, poderia ser usada com finalidades melhores numa instalação industrial. A soma vetorial da potência ativa com a potência reativa nos dá a potência real, conforme mostra a figura 22.
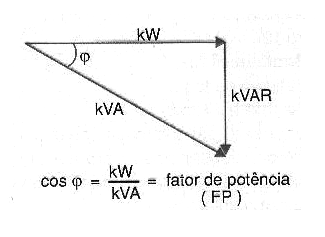
Veja que, se a potência reativa for pequena, o ângulo entre a potência real e a potência ativa diminui, indicando um uso mais eficiente da energia.
Assim, em lugar de se especificar a potência ativa ou a potência reativa, é comum indicar-se a eficiência no fornecimento e uso da energia pelo cosseno do ângulo mostrado na figura 190. Esse ângulo, denominado ? (phi), letra grega que se pronuncia “fi”, tem seu cosseno se aproximando de 1 quando ele tende a zero e ele define o fator de potência.
Desta forma, considerando-se que na figura, esse ângulo pode assumir valores entre 0 e 90 graus, seu cosseno variará entre 0 e 1, conforme mostra a figura 23.
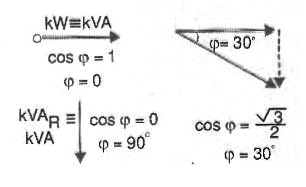
Podemos então dizer que o cosseno de ? pode variar entre 0 e 1. Tanto melhor será o aproveitamento da energia quanto mais próximo o fator de potência (FP) estiver próximo de 1, que é o valor ideal.
Também é possível medir o fator de potência como a relação entre a potência ativa e a reativa.
Assim, nas contas de energia temos a especificação dos kVA, mas sim os kVARh (quilowatts-reativos x hora) e os kWh (quilowatts x hora). Para se calcular o fator de potência, deve-se aplicar a seguinte fórmula:
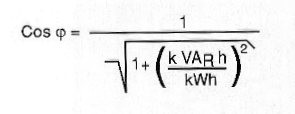
É importante observar que tudo isso é válido quando a energia está dentro dos padrões de qualidade que essas aplicações exigem.
A presença de harmônicas numa instalação altera tudo isso, e a fórmula acima não pode ser aplicada.
Impedância
Quando tratamos de circuitos que usam somente resistências puras, ou seja, componentes que se comportam como resistores, podemos aplicar a Lei de Ohm, sem problemas, para calcular seu comportamento elétrico.
No entanto, se tivermos um circuito de corrente alternada e em lugar de apenas resistores encontrarmos também indutores e capacitores, a Lei de Ohm, como a conhecemos já não vale.
Se tivermos somente capacitores ou somente indutores, podemos utilizar as fórmulas de reatância capacitiva e indutiva, conforme estudamos, mas tudo isso muda quando combinamos esses componentes, obtendo assim circuitos RLC.
Se, por um lado os capacitores têm a corrente adiantando-se em relação à tensão e os indutores atrasando, enquanto os resistores as têm em fase, como combinar tudo isso para obter os efeitos finais no comportamento desse circuito?
O efeito conjunto é denominado "impedância", podendo ser dito que corresponde de uma forma simplificada à "resistência" que um circuito apresenta a uma corrente alternada. Evidentemente, a impedância, apesar de medida em ohms não representa apenas uma simples oposição à passagem da corrente, pois ela leva em conta efeitos sobre a fase da corrente em relação à tensão.
Um exemplo de como a impedância pode ser calculada é dado inicialmente combinando-se um resistor e um capacitor, conforme o leitor poderá ver na figura 24.
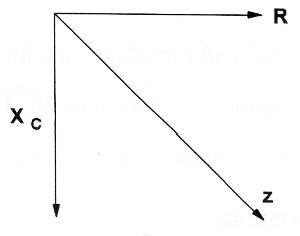
O resistor apresenta uma resistência pura (ôhmica) enquanto que o capacitor tem uma reatância capacitiva. As duas possuem efeitos diferentes no circuito que, colocados num gráfico ficam deslocados de 90 graus um do outro.
Isso significa que o resultado dos efeitos é uma soma vetorial, ou seja, uma soma que leva em conta a direção e o sentido dos efeitos no gráfico.
Assim, chamando a impedância de Z, a resistência de R e a reatância capacitiva de C nesse circuito, calculamos Z pela fórmula abaixo:
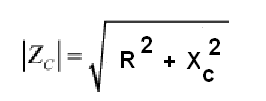
Onde:
Z é a impedância (em ohms)
R é a resistência (em ohms)
Xc é a reatância capacitiva (em ohms)
Podemos também ter o caso de um circuito formado por um indutor e um resistor, conforme mostra a figura 25.
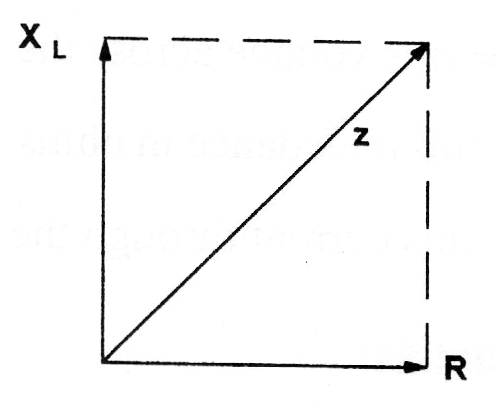
Nesse caso, a reatância indutiva será representada de forma diferente, conforme poderemos ver na mesma figura a resultante que é a impedância.
Chamando de Z a impedância, R a resistência e XL a reatância indutiva, podemos calcular a impedância pela fórmula abaixo:
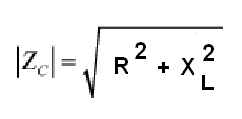
Onde:
Z é a impedância (em ohms)
R é a resistência (em ohms)
XL é a reatância indutiva (em ohms)
Finalmente, temos o caso em que o circuito é formado por um resistor, um indutor e um capacitor como poderá ser visto na figura 26.
Trata-se de um circuito RLC em que os efeitos das reatâncias e da resistência são colocados na forma gráfica conforme mostra a figura 27.
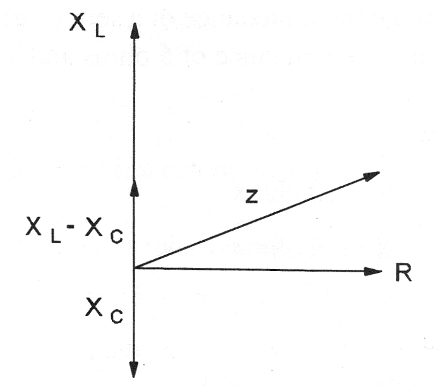
A impedância desse circuito pode ser calculada pela seguinte fórmula:
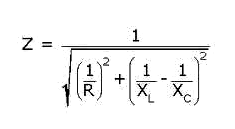
Onde:
Z é a impedância (em ohms)
R é a resistência (em ohms)
Xc é a reatância capacitiva (em ohms)
XL é a reatância indutiva (em ohms)
Observe que a soma da reatância capacitiva com a indutiva é uma soma vetorial, ou seja, devem ser considerados os sinais das grandezas.
Múltiplos e Submúltiplos das Unidades de Potência, Corrente e tensão
Para as unidades de corrente, tensão e potência que estamos usando é
comum usarmos múltiplos e submúltiplos para expressar ou valores muito grandes ou muito pequenos.
A seguir damos os múltiplos e submúltiplos mais usados:
a) CORRENTE
Unidade: ampère (equivale a passagem de uma carga de 1 Coulomb por segundo por um ponto de um condutor)
Abreviação: A
Submúltiplos mais usados:
1 miliampère (mA) = 0,001 A ou 1 milésimo de ampère
1 microampère (uA) = 0,000 001 A ou 1 milionésimo de
ampère
1 nanoampère (nA) = 0,000 000 001 A ou 1 bilionésimo
de ampère
1 picoampère (pA) = 0,000 000 000 001 A ou 1
trilionésimo de ampère
b) TENSÃO
Unidade: volt (equivale à tensão que aplicada a um condutor de 1 ohm de resistência faz fluir uma corrente de 1 ampère)
Abreviação: V
Múltiplos e submúltiplos:
1 microvolt (uV) = 0,000 001 V ou 1 milionésimo de volt
1 milivolt (mV) = 0,001 V ou 1 milésimo de volt
1 quilovolt (kV) = 1 000 V
1 megavolt (MV) = 1 000 000 V
c) POTÊNCIA
Unidade: watt (equivale a produção de 1 joule por segundo)
Abreviação: W
Múltiplos e submúltiplos:
1 picowatt (pW) = 0,000 000 000 001 W ou 1 trilionésimo de watt
1 nanowatt (nW) = 0,000 000 001 W ou 1 bilionésimo de watt
1 microwatt (uW) = 0,000 001 W ou 1 milionésimo de watt
1 miliwatt (mW) = 0,001 W ou 1 milésimo de watt
1 quilowatt (kW) = 1 000 W
1 Megawatt (MW) = 1 000 000 W
1 Gigawatt (GW) = 1 000 000 000 W
Unidades do SI - No Sistema Internacional de Unidades, as unidades básicas são:
| Grandeza Básica | Nome | Símbolo |
| Comprimento | metro | m |
| Massa | quilograma | kg |
| Corrente elétrica | ampère | A |
| Tempo | segundo | s |
| Temperatura termodinâmica | kelvin | K |
| Quantidade de substância | mol | mol |
| Intensidade luminosa | candela | cd |
Unidades derivadas do SI
| Grandeza derivada | Nome | Símbolo |
| Área | metro quadrado | m2 |
| Volume | metro cúbico | m3 |
| Velocidade | metro por segundo | m/s |
| Aceleração | metro por segundo ao quadrado | m/s2 |
| Número de onda | metro recíproco | m-1 |
| Densidade de massa | Quilograma por metro cúbico | kg/m3 |
| Volume específico | Metro cúbico por quilograma | m3/kg |
| Densidade de corrente | ampère por metro quadrado | A/m2 |
| Intensidade de campo magnético | ampère por metro | A/m |
| Concentração de substância | mol por metro cúbico | mol/m3 |
| Luminância | candela por metro quadrado | cd/m2 |
| Fração de massa | Quilograma por quilograma (*) | 1 |
(*) Deve ser representada pelo número 1