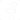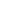Não é nada fácil escrever um artigo sobre resistência reatância e fator "Q" sem empregar fórmulas e que possa ser compreendido pela maioria daqueles que se interessam de uma ou de outra forma pela eletrônica, os quais nem sempre dispõem de conhecimentos suficientes no campo da matemática. Mas não será, assim espero, por esta simples razão que deixarão de entender estes conceitos básicos ainda que no decorrer do texto tenham escapado algumas fórmulas e expressões matemáticas, visando corresponder aos leitores mais acadêmicos, que irão envolver quatro a cinco operações aritméticas.
Nota: Artigo da revista Saber Eletrônica de maio de 1980.
Vejamos então a conceituação teórica destes termos técnicos largamente utilizados na prática.
A resistência é a oposição ou dificuldade que a corrente elétrica, contínua ou alternada, encontra para circular através de um condutor. Esta resistência elétrica pode ser comparada à "resistência" (atrito) que o solo oferece quando um veículo está em movimento ou mesmo à resistência oferecida pelo ar tendendo obstruir ou dificultar o movimento do veículo.
A resistência (elétrica) é medida em ohms (Ω) com seus múltiplos e submúltiplos mais usuais: megohm (MΩ), quilohms (kΩ) e miliohm (mΩ).
Esta dificuldade que a corrente encontra para circular por um condutor deve-se às sucessivas interações entre os elétrons que dão formação à corrente elétrica e os átomos que compõem o material condutor. Estes sucessivos choques obstruem a passagem de corrente gerando simultaneamente calor e, portanto, perde-se em energia calorífera (efeito Joule) parte da energia elétrica transmitida. A energia P perdida por calor em um condutor de resistência R quando é percorrido por uma corrente I é determinada matematicamente por:
P = 12R (I)
P em watts se I e R estiverem, respectivamente, expressos em ampères e ohms. Pela lei de ohm (V= IR), a expressão (1) acima também poderá assumir um dos seguintes aspectos:
P = V2 / R (II)
ou
P = VI (III)
em que V representa a queda de potencial nos extremos da resistência.
A reatância, similarmente à resistência, é a oposição apresentada pelos condutores à passagem de corrente alternada, isto é, correntes que variam de polaridade a cada meio ciclo. Porém, contrariamente à resistência, a reatância se apresenta como uma forma de armazenamento de energia que se acumula quando a corrente alternada atinge o pico máximo, retornando ao circuito quando a corrente decresce. Este fenômeno pode ser comparado a um automóvel: este se movimenta porque recebe energia proveniente do combustível, quando retiramos o pé do acelerador e situamos o carro no "ponto morto" ou mesmo se "desligarmos a máquina", o carro continua a movimentar-se por determinado tempo devido ao efeito de inércia, isto equivale a dizer que, mesmo faltando energia externa, continua existindo energia no "circuito" provocando o movimento. De qualquer forma, o movimento irá cessar porque existem perdas de energia devido ao atrito dos pneus com o solo e da resistência oferecida pelo ar que é proporcional à velocidade desenvolvida; da mesma forma, quando cessa a corrente elétrica em um circuito elétrico, continua a existir energia no mesmo, a qual irá diminuindo gradativamente devido às perdas provocadas pela resistência (elétrica) do mesmo - se somente existisse reatância, o circuito seria ideal e não haveria perdas, mas na prática, sempre existem perdas.
Assim como a resistência, a reatância é expressa em ohms (ohms), apresentando os mesmos múltiplos e submúltiplos que ela.
Existem dois tipos de reatância: reatância capacitiva e reatância indutiva; na primeira, a reatância é inversamente proporcional à frequência (quanto maior a frequência menor é a reatância capacitiva, e vice-versa); como a própria designação sugere, esta reatância refere-se a capacitores. A reatância indutiva é diretamente proporcional à frequência da corrente - a reatância indutiva é uma característica inerente aos indutores ou bobinas.
Tanto a reatância capacitiva como a indutiva podem ser determinadas, em módulo, pelas seguintes expressões: para a reatância capacitiva
XC = 1 / (2 π f C) - (IV)
e para a reatância indutiva
XL = 2 π f L (V)
onde
Xc - reatância capacitiva ( Ω ),
XL - reatância indutiva ( Ω ),
C - capacitância (farads),
L - indutância (henrys),
? - constante (2--3,14)
f - frequência (Hz) da corrente ou tensão
Exemplos:
1) A reatância de um capacitor (reatância capacitiva) de 4,7 N F à frequência de 2 kHz vale, de acordo com (IV):
XC = 1 / (2 x 3,14 x 2x103 x 4,7x10-6)
XC = 1 / (6,28 x 2x103 x 4,7x10-6)
XC = 17 ohms
A reatância deste mesmo capacitor à frequência de 200 kHz será:
XC = 1 / (2 x 3,14 x 200x103 x 4,7x10-6)
XC = 1 / (6,28 x 2x105 x 4,7x10-6)
XC = 0,17 ohms
Os resultados confirmam que com o aumento da frequência a reatância capacitiva diminui, e vice-versa.
2) A reatância indutiva de um indutor de 1,5 mH à frequência de 20 kHz será, de acordo com (V):
XL = 2 x 3,14 x 20x103 x 1,5x10-3
XL = 6,28 x 2x104 x 1,5x10-3
XL = 188,4 ohms
A reatância deste mesmo indutor à frequência de 80 kHz valerá:
XL = 2 x 3,14 x 80x103 x 1,5x10-3
XL = 6,28 x 8x104 x 1,5x10-3
XL = 753,6 ohms
Os resultados obtidos confirmam o que se havia dito anteriormente: a reatância indutiva aumenta com a frequência, ou seja, a reatância indutiva é diretamente proporcional à frequência.
O efeito combinado da resistência e reatância, é denominado impedância, sendo usualmente representado pela letra Z, assim:
Z = R + X (VI)
onde R e X representam, respectivamente, a resistência e a reatância.
Ainda que R e X tenham a mesma unidade (ohm), não poderemos somá-las conforme sugere a expressão acima, isto porque as duas grandezas em pauta representam dois fenômenos físicos de significado totalmente diverso um do outro pois, como sabemos, a resistência traduz uma perda, digamos, constante, enquanto a reatância é uma forma de armazenamento de energia. Em realidade, a resistência é representada graficamente no eixo “x” (eixo horizontal) e a reatância no eixo “y" (eixo vertical) conforme ilustra a figura 1. A impedância será então representada pela reta que une a origem do sistema de eixos! ponto 0) à interseção da vertical traçada por R com a horizontal que passa por X - figura 2. Nestas condições, pelo teorema de Pitágoras, o valor da impedância (em ohms) é calculado por:
Z = √(R2 + X2) - (VII)
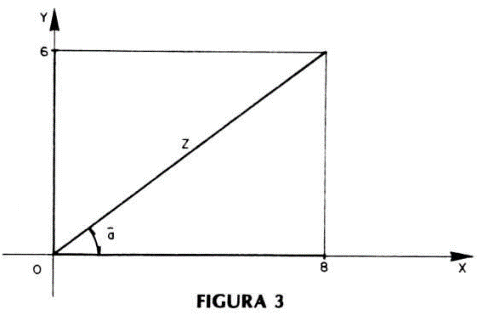
Assim, se por exemplo, tivermos um circuito com uma resistência igual a 8 ? e uma reatância de 611 (figura 3), o valor da 'impedância do circuito em pauta será de:
Z =√(82 + 62)
Z = √(64 + 36)
Z = √(100)
Z = 10 ohms
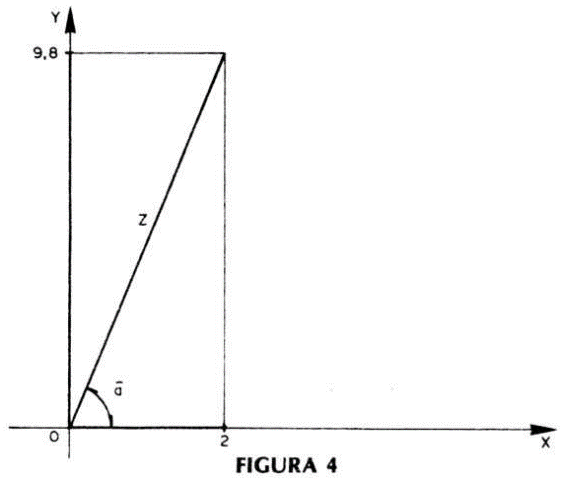
Da mesma forma para R= 2 e X = 9,8 (figura 4), teremos:
Z = √(22 + 9,82)
Z = √(4 + 96,04)
Z = 10 ohms
Observamos nestes dois exemplos que o valor da impedância é o mesmo para os dois casos, porém o segundo trata de um circuito mais reativo que o primeiro, aliás, isto pode ser observado à partir do ângulo a que a reta representativa da impedância forma com o eixo resistivo (eixo x, horizontal): no primeiro exemplo o ângulo é menor que no segundo e, portanto, o circuito é menos reativo que o segundo.
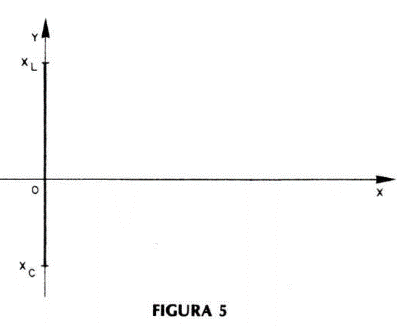
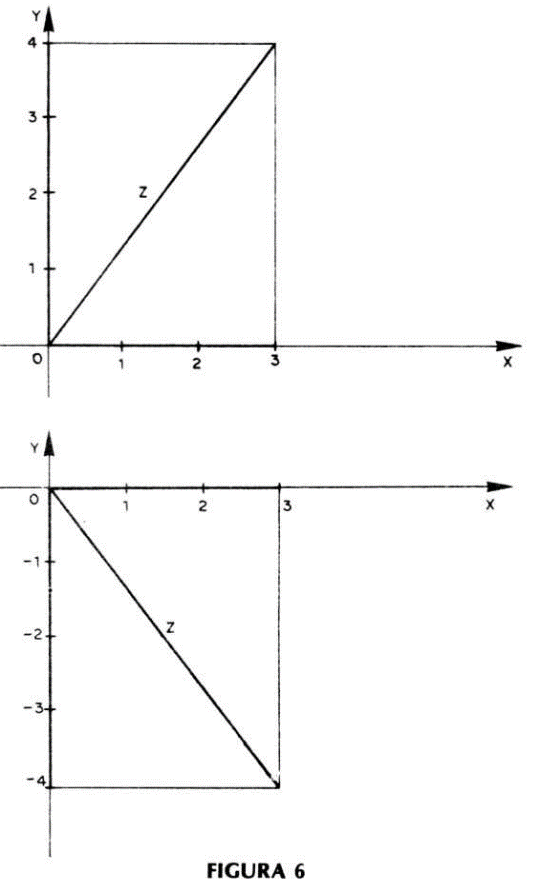
Graficamente representamos a reatância indutiva no semieixo positivo y e a reatância capacitiva no semieixo negativo conforme ilustra a figura 5. A soma algébrica destas reatâncias de um circuito hipotético, poderá ser negativa, positiva ou nula. Se negativa, dizemos que o circuito é reativamente capacitivo; se positiva, dizemos que o circuito é indutivo e se nula, que o circuito é puramente resistivo. Desta forma a impedância Z = 4 + 3 j corresponde a um circuito indutivo e a impedância Z = 4 -3j corresponde a um circuito capacitivo - figura 6.
Obs: A letra j (operador j) indica que seu coeficiente associado deve ser marcado num sistema cartesiano no eixo vertical.
Como vimos, a reatância indutiva de uma bobina e a reatância capacitiva de um capacitor são afetadas de forma oposta pela frequência, isto quer dizer que um determinado circuito LC existe uma frequência tal que as reatâncias são iguais em módulo, porém de sinais contrários e por isto se anulam, neste caso a componente reativa da impedância é nula, existindo apenas a componente resistiva. É justamente neste caso que se verifica o ponto de ressonância do circuito, isto é, quando as reatâncias indutiva e capacitiva se anulam, oferecendo menor oposição à passagem da corrente.
Os circuitos de ressonância podem ser do tipo paralelo (figura 7) ou do tipo série (figura 8).
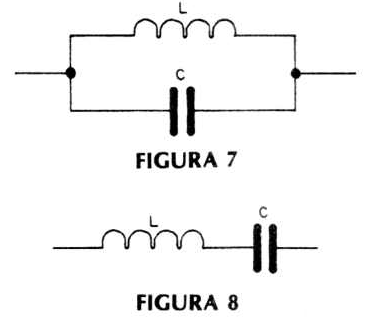
Para o circuito ressonante paralelo da figura 7, se C = 10 µF e L = 30 mH, o ponto de ressonância será dado quando XL + XC = 0, conforme vimos acima, assim:
XL = XC → 2 π fL = 1 / (2 π f C)
Um simples algebrismo nos permite escrever:
f = 1 / [ 2 π √(LC) ] - (VIII)
onde f é a frequência de ressonância do circuito. De acordo com os valores fornecidos para L e C, temos:
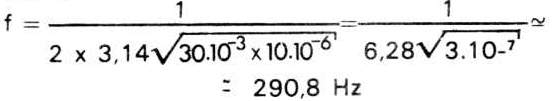
que é a única frequência em que as reatâncias capacitiva e indutiva se anulam.
Da mesma forma para o circuito ressonante tipo série da figura 8, a frequência de ressonância será de 2322,7 Hz quando C = 47 nF e L = 100 mH, pois de acordo com a expressão (VIII) teremos:

Para ambos circuitos, quanto menor forem os valores de C e L tão maior será a frequência de ressonância do circuito.
Um circuito ressonante nada mais é do que uma célula LC que armazena energia em determinados instantes e em outros devolve essa energia para o circuito externo: o capacitor irá armazenar energia elétrica enquanto a bobina armazenará energia magnética que, em última análise, o primeiro fornecerá "tensão" enquanto o indutor, corrente. Entre os dois componentes constantemente haverá uma troca de energia, ora o capacitor está carregado e o indutor descarregado, imediatamente a seguir, o capacitor estará descarregado e o indutor carregado, provocando, desta forma, uma série interminável de oscilações se ambos componentes forem ideais, ou seja, não apresentam componente resistiva associada. Acontece que na prática isto não acontece pois ao capacitor está associada uma outra resistência proveniente do próprio condutor que compõe a bobina; por esta razão as oscilações acima mencionadas tendem a esgotar-se já que as componentes resistivas das células L e C se encarregam de transformar a energia do circuito, em calor (efeito Joule) até que a energia total do sistema seja nula.
Do exposto concluímos que uma célula ressonante será tão melhor quanto tão menor for a sua componente resistiva ou, em outras palavras, quanto mais alto for a relação entre a energia armazenada e a energia dissipada.
A relação entre a energia armazenada e a energia dissipada, dá-se o nome de fator "Q" do circuito.
É claro que na maioria dos projetos destas células, deveremos fazer com que a mesma apresente um elevado valor para o fator "Q", o qual é proporciona; à reatância do circuito e inversamente proporcional à sua resistência.
A proporção que a amplitude da corrente se extingue em um circuito ressonante depois que a fonte de energia foi removida, ocorre o decremento ou amortecimento. Um circuito que possui alto decremento (baixo "Cr), diz-se que tem um amortecimento elevado; com baixo decremento (alto "O"), diz-se que ele tem um amortecimento reduzido.