Para a medida de frequências com a ajuda do osciloscópio é imprescindível o conhecimento das figuras de Lissajous. Mas, mais do que isso, elas representam uma interessante forma de composição de sinais senoidais, que deve ser estudada por todos. Neste artigo mostramos como são produzidas estas figuras e o que elas significam,
A maioria dos sinais elétricos com que trabalhamos possui forma de onda senoidal, conforme ilustrado na figura 1.
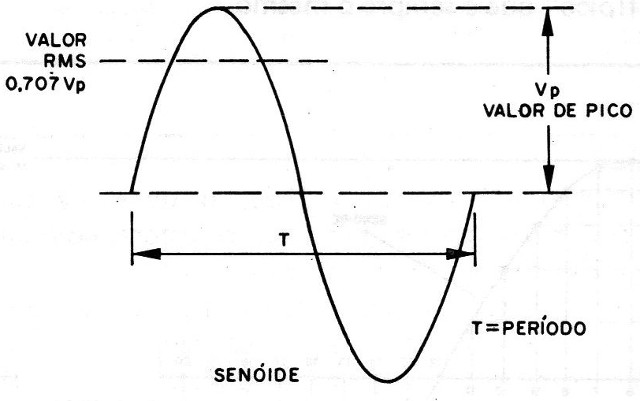
Esta forma indica o modo como este sinal varia em cada instante.
Pode representar o valor, em cada instante, de uma tensão ou de uma corrente.
Qual é a origem desta forma de onda? O que significa que um sinal tem uma forma de onda senoidal?
A SENÓIDE
Imaginemos um ponto P que gira com velocidades uniforme, realizando uma trajetória perfeitamente circular, conforme mostra a figura 2.
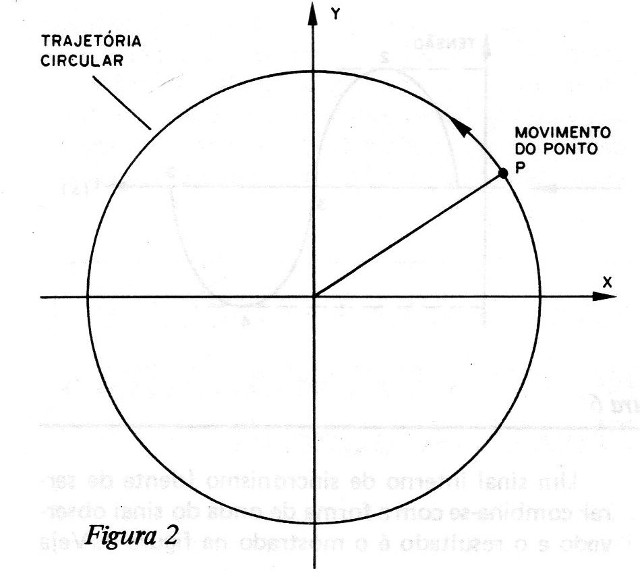
Partindo do ponto O, podemos medir (ou indicar) a posição deste ponto por meio de um ângulo que é formado pela linha que liga este ponto ao centro do círculo, que é sua trajetória, e pelo eixo X de referência conforme mostra a figura 3.
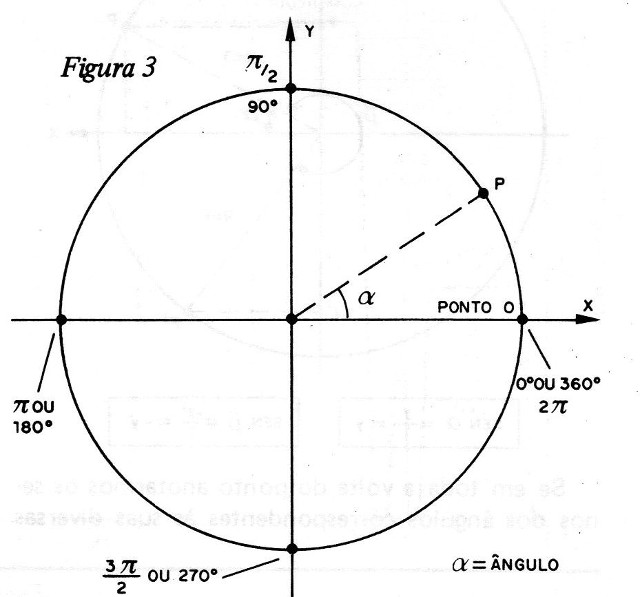
Vemos então que 1/4 'de volta corresponde a 90° e que a volta inteira ou um ciclo de seu movimento corresponde a 360°.
Podemos também usar uma outra forma de medida para o movimento deste ponto P.
Levando em conta que o comprimento de uma circunferência é numericamente igual a duas vezes o seu raio multiplicado pelo fator PI (3,14) podemos medir a circunferência em “radianos", ou seja, em frações ou múltiplos de seu próprio raio.
Assim, como a volta inteira corresponde a 2pi radianos, facilmente estabelecemos relações desta grandeza com os graus:
90 graus -> pi/2 radianos
180 graus -> pi radianos
2709raus -> 3pir/2 radianos
360 graus -› 2pi radianos
As duas formas de medida são usadas em eletrônica.
Importante é prosseguirmos com o nosso ponto em movimento para ver o que acontece realmente.
Em cada instante do seu movimento podemos tirar a projeção sobre o eixo Y, de modo a obter uma “altura" sobre X.
Esta distância, mostrada na figura 4, variará em toda a volta, adquirindo ora valores positivos e ora valores negativos.
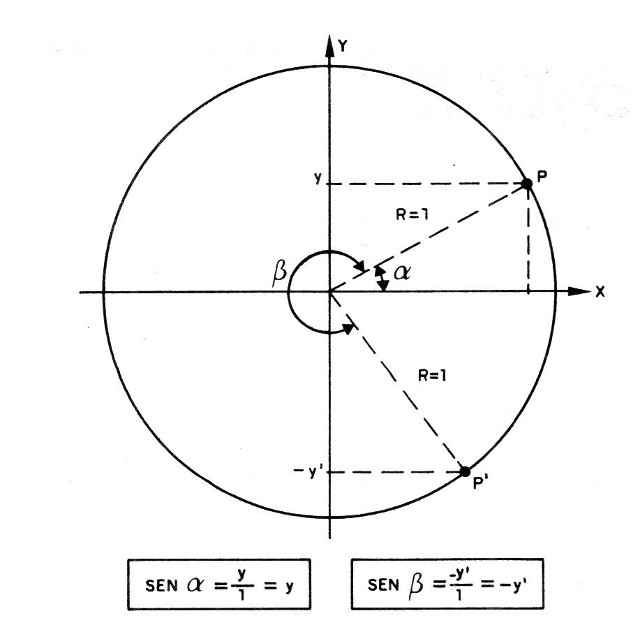
Se considerarmos unitário o raio da circunferência, esta distância Y para cada posição do ponto nos dará uma grandeza chamada “seno", ou abreviadamente sen, do ângulo correspondente.
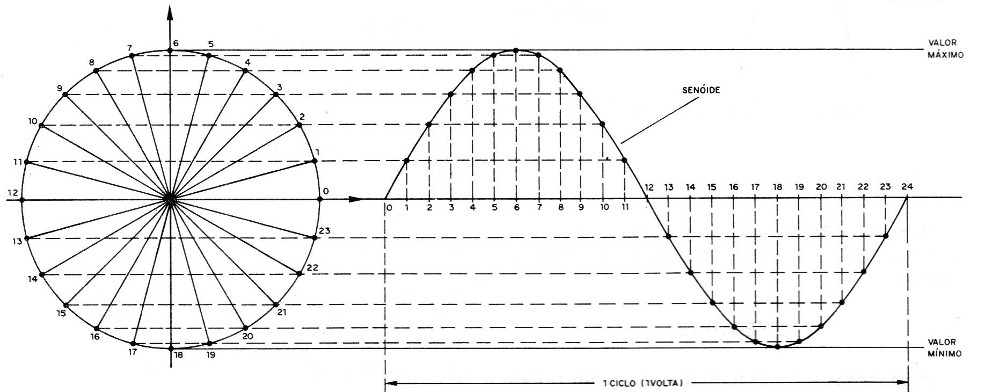
Se em toda a volta do ponto anotarmos os senos dos ângulos correspondentes às suas diversas posições, obtemos uma figura ondulada, conforme mostra a figura 5.
Esta figura denomina-se “senóide" e representa justamente a variação da projeção de P sobre o eixo Y.
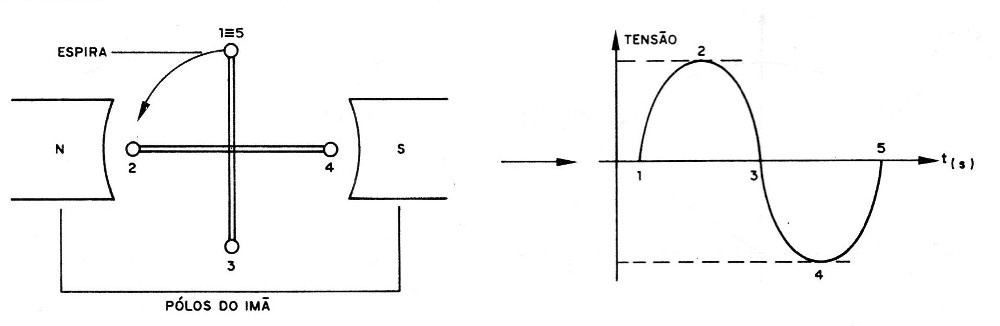
Se tivermos um gerador que corresponda a uma espira que gire no campo magnético de um ímã, conforme mostra a figura 6, a indução de corrente em cada instante pode ser comparada à projeção do ponto P.
Levantando então a curva do sinal produzido por este gerador, em cada posição da espira, obtemos então uma tensão que varia conforme uma senóide.
Os circuitos oscilantes também geram tensões que variam no tempo segundo curva semelhante.
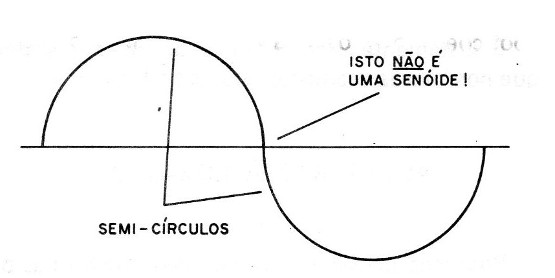
Neste ponto, chamamos a atenção para os leitores que devem ver que a curvatura da senóide não corresponde realmente à meias circunferências, como mostrado na figura 7, mas tem um formato típico que é sempre o mesmo.
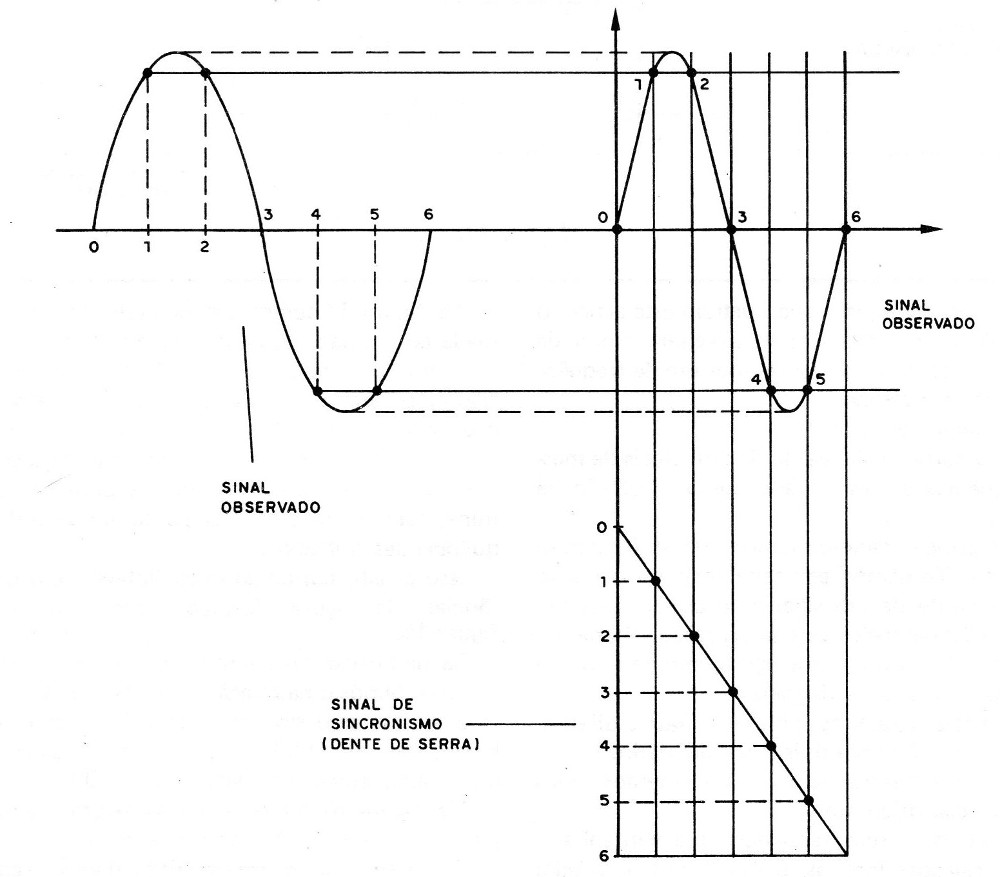
Os osciloscópios são instrumentos que possibilitam a visualização da forma de onda de um sinal (figura 8).
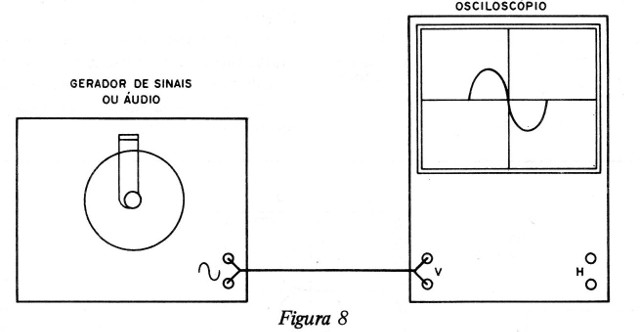
Um sinal interno de sincronismo (dente de serra) combina-se com a forma de onda do sinal observado e o resultado é mostrado na figura 9.
Veja então que dente de serra mais qualquer forma de onda, resulta nesta qualquer forma de onda.
O que acontece se combinarmos dois sinais senoidais, em lugar de uma forma de onda qualquer, com um sinal dente de serra?
Podemos pensar neste fenômeno não só em termos elétricos, mas até em termos de movimentos de objetos mecânicos.
Qual seria a imagem projetada por duas circunferências que girassem uma sobre a outra, conforme mostra a figura 10?
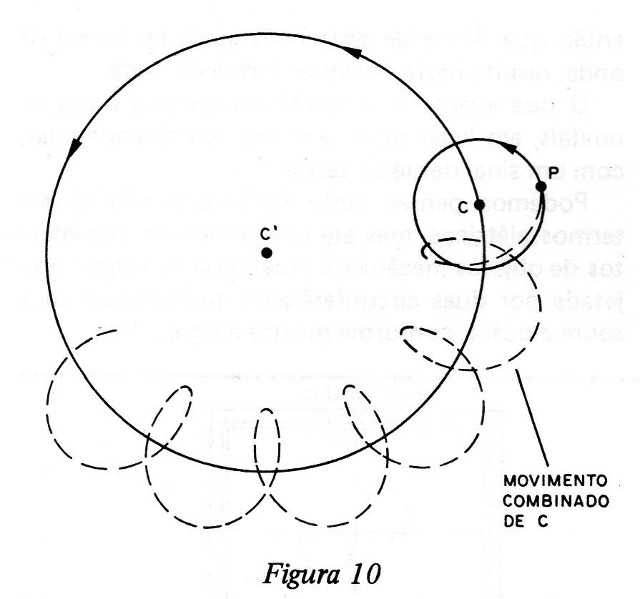
É justamente a composição de sinais senoidais que nos leva às chamadas figuras de Lissajous.
AS FIGURAS DE LISSAJOUS
Podemos pensar na composição das formas de onda senoidais como a sua "mistura". É como se tivéssemos um mixer capaz de juntar dois sinais de características diferentes, obtendo-se um efeito final diferente.
Podemos visualizar o que ocorre de uma forma muito simples, usando para isso o osciloscópio.
Ligamos um dos sinais na entrada vertical e o outro na entrada horizontal, desligando o sincronismo interno. (figura 11)
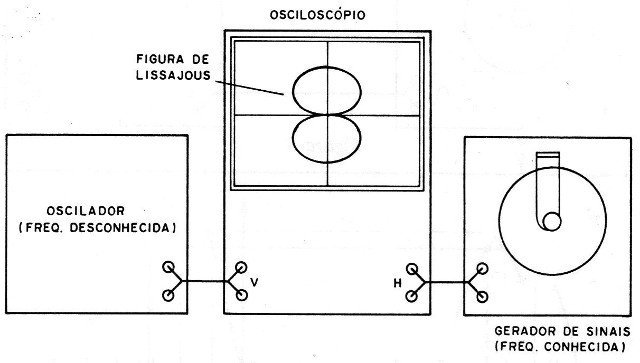
Para “ver" as figuras que ilustram este artigo, o leitor, além do osciloscópio, precisará ainda de dois geradores de sinais (pode usar um de frequência fixa e outro variável).
O que acontece então?
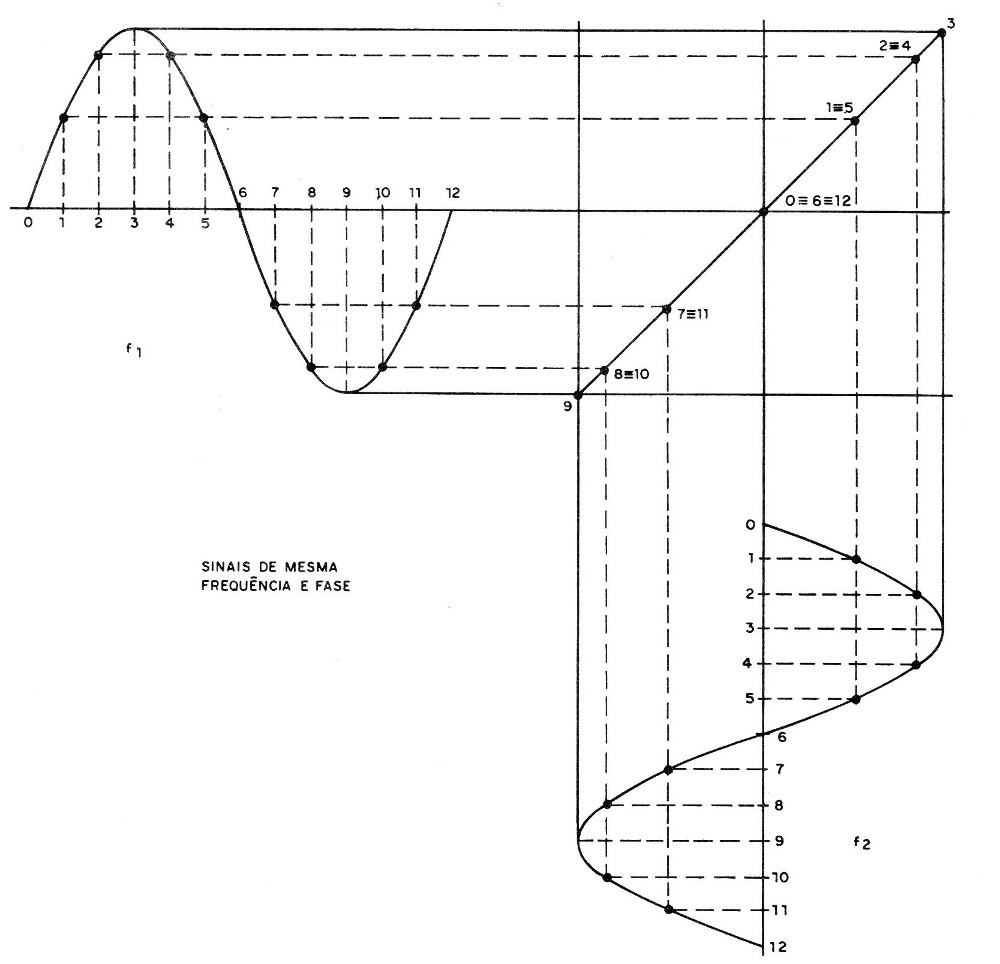
Vamos partir inicialmente de dois sinais de mesma frequência e mesma fase, como mostrado na figura 12.
A composição para estudá-lo pode ser feita ponto-a-ponto. Tomamos em cada instante o ponto correspondente de um sinal e do outro, traçando linhas perpendiculares, que se cruzarão.
Numerando estas linhas, obtemos a figura completa, que é um traço inclinado de 45 graus.
Para sinais defasados, obtemos figuras diferentes. Na figura 13 temos o resultado de dois sinais defasados.
Mas, o interessante ocorre quando temos sinais de frequências diferentes.
Se os sinais tiverem frequências que mantenham, entre si, relações inteiras, como 2 para 1, 3 para 2, 5 para 4, 7 para 2, as figuras formadas adquirem aspectos interessantes.
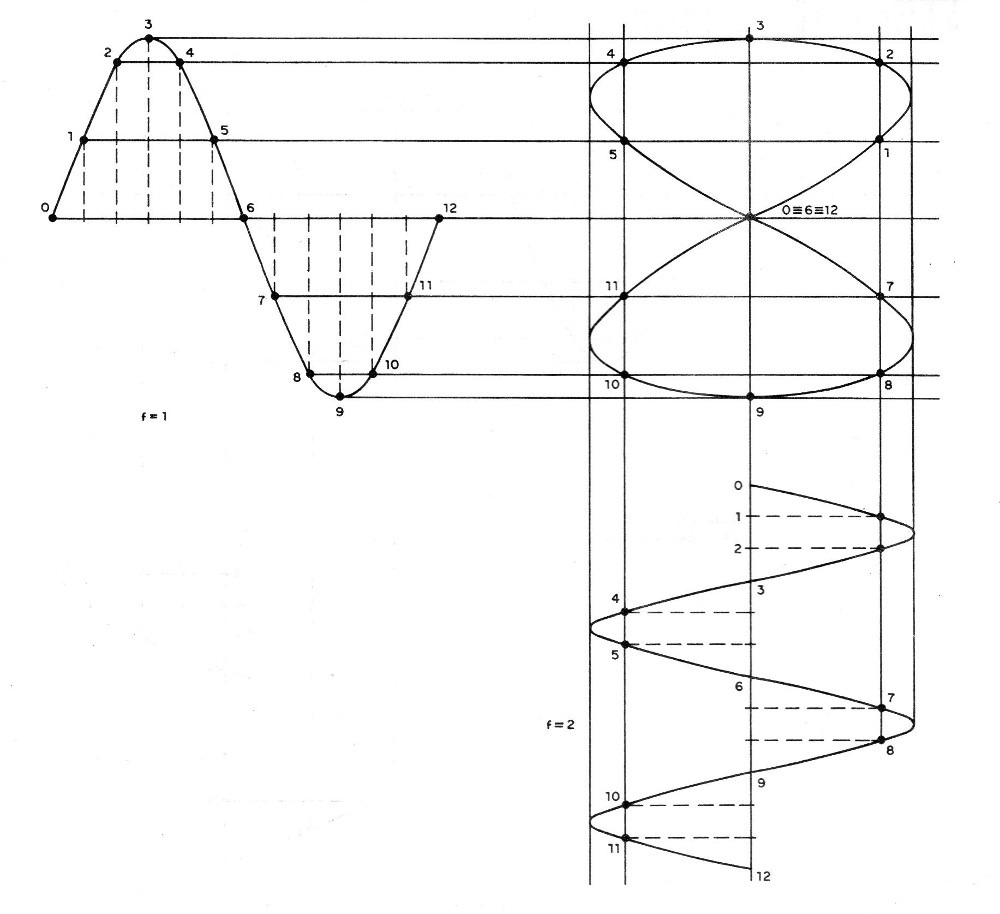
Na figura 14 temos um exemplo de figura formada com uma relação de frequências de 2 para 1.
O interessante é que, através da observação da figura, podemos justamente determinar esta relação de frequência.
Assim, se tivermos um osciloscópio e um gerador de sinais de frequência conhecida, observando a figura formada, podemos determinar facilmente a frequência de um sinal de frequência desconhecida.
Isso é feito contando-se os “lobos" ou protuberâncias da figura formada, como mostra a figura 15.
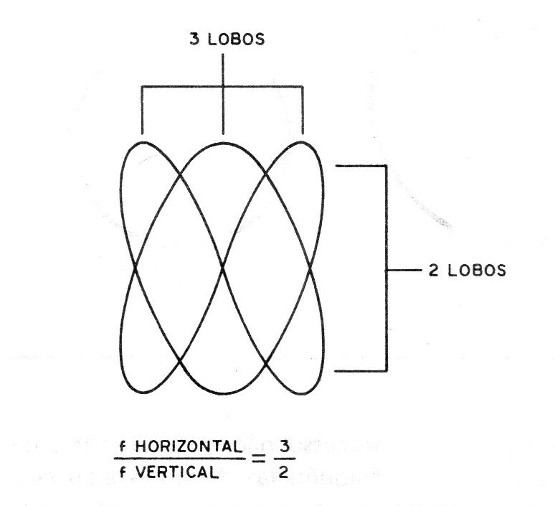
Se na horizontal tivermos 3 lobos e na vertical 2 lobos, temos uma relação de frequências de 3 para 2.
Assim, se o sinal conhecido for o aplicado na horizontal, de 1500 Hz, por exemplo, saberemos que o sinal aplicado na vertical é de 1 000 Hz.
Na figura 16 temos diversas figuras formadas para diferentes relações de frequências.
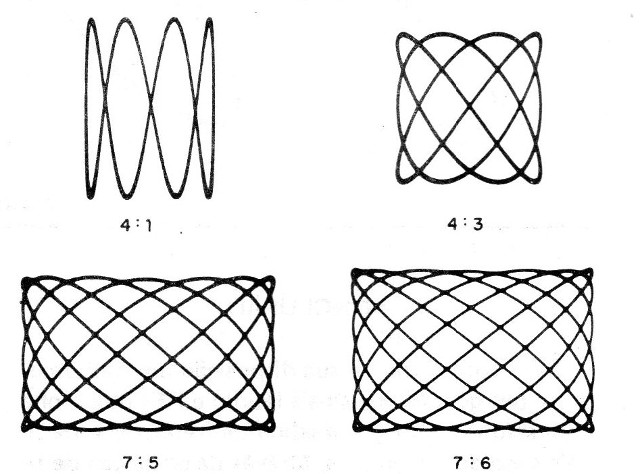
Do mesmo modo, para sinais de mesma frequência, conforme a figura formada podemos verificar sua defasagem.
CONCLUSÃO
Se o leitor tiver à sua disposição um osciloscópio e um gerador de sinais (áudio e RF) que tenha uma saída senoidal, a medida de frequências de sinais senoidais é simples, através da obtenção de figuras de Lissajous.
Na verdade, o processo não é válido somente para a medida de frequências de sinais elétricos.
Fenômenos periódicos que sigam a lei do seno, como a oscilação de pêndulos, molas, vibração de lâminas, etc., podem, com a ajuda de transdutores, serem analisados do mesmo modo.