Uma comparação que temos feito, e que muitos outros fazem, com o aparecimento no mercado de supercapacitores com mais de 10F é que, se fossem elaborados com a tecnologia convencional, seriam do tamanho da terra. Já recebemos até mensagens dizendo que isso é um exagero, e que não corresponde à realidade. Neste artigo vamos provar que um capacitor de 1F seria não apenas do tamanho da terra, mas muito maior.
O ensino de física parte de princípios muito bem estabelecidos através de anos de estudos. É o caso da eletricidade estática que aprendemos no ensino fundamental pela eletrização de objetos e depois no ensino médio com cálculos envolvendo forças, campos e potenciais.
Nesses estudos, um ponto importante que serve para a eletrônica é o que trata das cargas armazenadas nos corpos e dos capacitores.
Assim, aprendemos que um corpo pode ser eletrizado, ou seja, pode armazenar cargas elétricas e que arranjos especiais de condutores e isolantes podem aumentar essa capacidade de armazenamento, levando aos componentes que hoje conhecemos como capacitores.
Para que então possamos matar nossa curiosidade sobre os capacitores do tamanho da terra, vamos partir de uma esfera de metal. Um condutor montado sobre um pedestal e que é usado em muitos experimentos de física nas escolas do segundo grau, cursos técnicos e mesmo superiores.
Ao ser carregada esta esfera está armazenando cargas elétrica, ou seja, é um capacitor esférico.

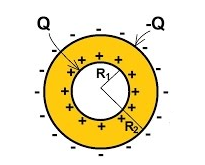
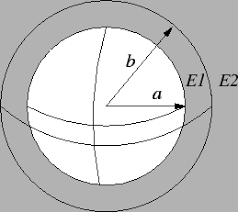
Aprendemos que um capacitor precisa ter duas armaduras, uma positiva e uma negativa, o que levaria a ideia de que um capacitor esférico, por exemplo, seria formado por dois condutores concêntricos, separados por um dielétrico, conforme mostra a figura 2.
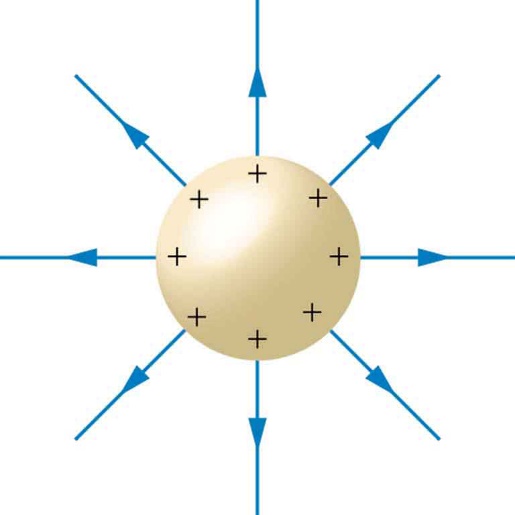
No entanto, também podemos considerar uma única esfera se ela for uma das armaduras e a outra estiver no infinito. Assim, as linhas de força do campo elétrico saem radialmente da esfera, como estamos acostumados a representar. A carga dessa esfera é a carga do capacitor.
A quantidade de cargas armazenadas divididas pela tensão em que se encontram nos dá a capacitância, pela conhecida fórmula:
C = Q/V
Vemos que essa capacitância C depende do tamanho da esfera.
Mas, num capacitor esférico, como podemos calcular a capacitância em função do seu tamanho.
Podemos escrever uma fórmula que diz qual é a capacitância em função da distância entre as armaduras até o centro da esfera:
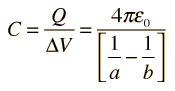
Esta fórmula, por exemplo, pode levar em conta que a ionosfera é uma camada de nossa atmosfera condutora e poderia ser usada na fórmula.
Mas, podemos simplificar essa fórmula, levando em conta apenas uma esfera do tamanho da terra, ou seja, um condutor esférico carregado.
Com isso, o termo b da fórmula tenderia ao infinito e com isso poderíamos ter 1/b = 0, eliminando esse termo. A fórmula ficaria:
C = 4Πε0a
Tudo bem, sabemos que Π vale 3,14, mas e esse fator esquisito ε o, do que se trata?
Trata-se de uma constante, algo muito comum nas fórmulas físicas.
Quando vamos quantificar algum fenômeno através de uma fórmula, fazemos experimentos e anotamos os resultados, usando unidades que estabelecemos. Por exemplo, medimos distâncias em metros, forças em Newtons etc.
No entanto, os resultados práticos nem sempre dão certo com valores que não correspondem à realidade que medimos. Assim, precisamos acrescentar nas fórmulas o fator que as adaptem às unidades usadas. Esse fator é um número que não muda.
O que sabemos é que, se não usamos essas constantes, a fórmula não funciona e se usarmos tudo fica de acordo com que observamos na prática. Na tabela abaixo temos alguns constantes que são usadas nos cálculos de física.
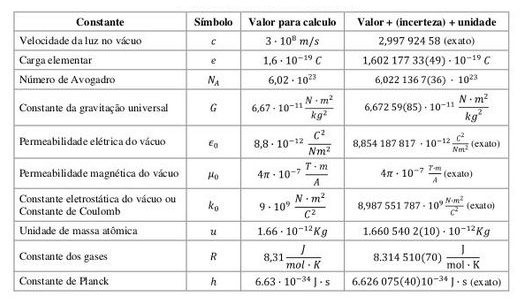
Veja que uma delas é justamente o εo. Trata-se da “constante dielétrica do vácuo” supondo que entre a terra e o infinito tenhamos mais vácuo do que atmosfera.
O valor foi obtido através de experimentações, sendo usado em qualquer cálculo que envolva capacitores, por exemplo, Seu valor:
εo = 8,852 x 10-12 (não vamos nos preocupar aqui com as unidades)
Assim, nos cálculos em que essa constante apareça, temos de substitui-la por esse valor.
Chegamos então ao ponto que interessa. Que capacitância teria uma esfera de metal do tamanho da terra?
Vamos adotar um raio aproximado de 6 000 km para a terra, ou 6 x 106 metros.
Temos então para nosso problema:
C = queremos calcular
Π= 3,14
A = 6 x 106
εo = 8,852 x 10-12
Colocando na fórmula temos:
C = 4Πε0a
C = 4 x 3,14 x 8,852 x 10-12 x 6 x 106
C = 0,67 x 10-3 F
C = 0,67 mF
Bem pequeno o valor, comparado a um supercapacitor.