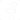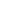Quando resistores estão ligados em série ou paralelo da maneira convencional, isto é, seguindo os padrões que facilmente podemos perceber que se encontram desse modo, a aplicação da fórmula é o único recurso necessário a obtenção da resistência equivalente.
Quando, entretanto, os resistores são ligados de modo um pouco mais disfarçado em que o técnico menos experiente sente dificuldade em saber como estão ligados,
Para se obter a resistência equivalente, a coisa se torna um pouco mais complicada o que ocorre no caso de uma associação que já vimos no site
Se bem que aparentemente os resistores estejam ligados em série, já que aparecem ”enfileirados" da maneira convencional, não é o que ocorre na realidade, dadas as ligações externas. Para a resolução deste teste temos, portanto, que usar de um artifício que consiste em transformar este circuito num equivalente em que o modo de ligação se torne visível.
Para isso, damos nomes aos nós, ou seja, pontos de interligações. Assim, o mesmo circuito, pode ser transformado no equivalente da figura, que. facilmente percebemos que se trata de uma ligação em paralelo.
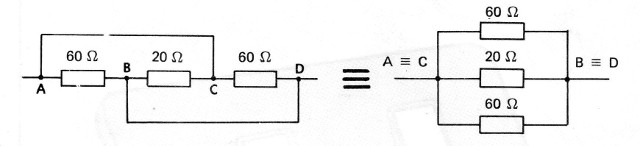
Assim,como se tratam de três resistores em paralelo, temos que aplicar a fórmula tradicional:
1/R = (1/R1) + (1/R2) + (1/R3)
1/R = (1/60) + (1/20) + (1/60)
Extraindo O mínimo múltiplo comum e reduzindo ao mesmo denominador temos:
1/R = (1 + 3 + 1) /60
1/R = 5/60
1/R = 1/12
Obtemos deste modo 1/ R ou seja, o inverso de R. Como, entretanto, queremos obter R, devemos inverter esse resultado de onde obtemos:
1/R = 1/12
R = 12/1
R = 12 ohms
que é a resposta correta para a questão proposta.